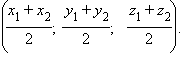10. Понятие базис.Разложение вектора по базису.

     Определение. Базисом в пространстве Rⁿ называется любая система из n-линейно независимых векторов. Каждый вектор из Rⁿ, не входящих в базис, можно представить в виде линейной комбинации базисных векторов, т.е. разложить по базису.      Пусть   – базис пространства Rⁿ и  . Тогда найдутся такие числа λ₁, λ₂, …, λ_n, что  .      Коэффициенты разложения λ₁, λ₂, …, λ_n, называются координатами вектора   в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.      Пример. Доказать, что векторы   образуют базис в R³.      Решение. Покажем, что равенство   возможно только при λ₁ = λ₂ = λ₃ =0:            или 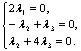      Решив систему, получим λ₁=0, λ₂=0, λ₃=0. Так как все λ_i=0 (i=1,2,3), то   - линейно независимы. Они могут составить базис в R³.      Очевидно, любой новый набор из векторов       может тоже быть взятым в качестве базиса в R³. Итак, базис может быть выбран неединственным образом.      Пример. Разложить вектор   по базису  .      Решение.  . Подставим координаты всех векторов и выполним действия над ними:            Приравняв координаты, получим систему уравнений: 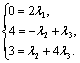           Решим ее:  .      Таким образом, получим разложение:  .      В базисе   вектор   имеет координаты  .     Замечание. В каждом n-мерном векторном пространстве можно выбрать бесчисленное множество различных базисов. В различных базисах один и тот же вектор имеет различные координаты, но единственные в выбранном базисе.

11.Декартовая система координат. Направление косинуса вектора.

Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат– и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. В конкретной невырожденной координатной системе каждой точке соответствует один и только один набор координат.

Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной). Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат (в честь французского математика Рене Декарта).

График 1.2.1.1. Декартова система координат

В элементарной математике чаще всего рассматривается двухмерная или трехмерная декартова система координат; координаты обычно обозначаются латинскими буквами x, y,z и называются, соответственно, абсциссой, ординатой и аппликатой. Координатная ось OX называется осью абсцисс, ось OY – осью ординат, ось OZ – осью аппликат. Положительные направления отсчета по каждой из осей обозначаются стрелками.

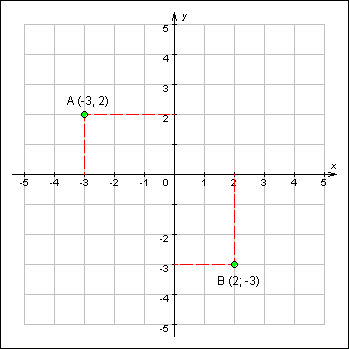
График 1.2.1.2. Координаты точки в декартовой системе координат. Важно отметить, что порядок записи координат существенен; так, например, точки A (–3; 2) и B (2; –3) – это две совершенно различные точки

Как определить координаты точки в декартовой системе координат? Проведем через точку A прямые (в трехмерном случае – плоскости), перпендикулярные осям. Расстояния от точек пересечения построенных прямых (плоскостей) с осями абсцисс, ординат (аппликат) до начала координат, взятые со знаком «+», если точки лежат на положительных полуосях, и со знаком «–», если они лежат на отрицательных полуосях, и будут координатами точки A. Координаты точки записываются в скобках: например, A (–3; 2) илиB (x₀; y₀). В трехмерном пространстве координаты точки в декартовой системе координат записываются тремя числами, например, C (5; 0,2; –6).

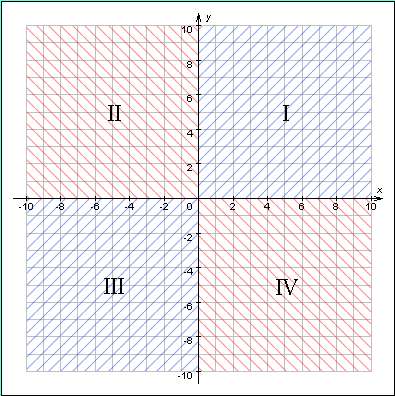
Рисунок 1.2.1.1. Координатные оси делят координатную плоскость на четыре квадранта (четверти). Точки, лежащие на осях координат, не принадлежат ни одному квадранту

В двухмерной системе координат все точки, лежащие над (под) осью OX, образуют верхнюю (нижнюю) координатную полуплоскость. Все точки, лежащие правее (левее) осиOY образуют правую (левую) координатную полуплоскость.

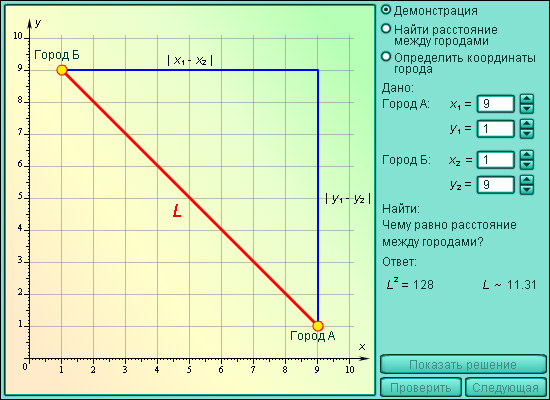
Модель 1.5. Расстояние между городами

В конце этого параграфа приведем некоторые очевидные формулы.

• Расстояние от точки A (x₀; y₀) до оси OX равно |y₀|.

• Расстояние от точки A (x₀; y₀) до оси OY равно |x₀|.

• Расстояние от точки 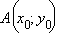  до начала координат равно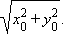 

• Расстояние |AB| между точками A (x₁; y₁) и B (x₂; y₂) равно 

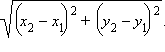
• Точка M, которая является серединой отрезка AB, где A (x₁; y₁) и B (x₂; y₂), имеет координаты 

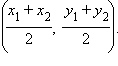
График 1.2.1.3. Координаты середины отрезка

На случай трехмерного пространства эти формулы обобщаются следующим образом:

• Расстояние от точки A (x; y; z) до плоскости OYZ равно |x|.

• Расстояние от точки A (x; y; z) до начала координат равно 

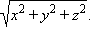
• Расстояние |AB| между точками A (x₁; y₁; z₁) и B (x₂; y₂; z₂) равно 

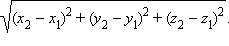
• Координаты точки M, которая является серединой отрезка AB, где A (x₁; y₁; z₁) и B (x₂; y₂; z₂) равны