8.Линейная зависимость векторов

Введем еще одно очень важное понятие, которое используется не только в алгебре, но и во многих других разделах математики.

        Определение 10.14   Система векторов   называется линейно зависимой, если существует такой набор коэффициентов   , из которых хотя бы один отличен от нуля, что   .         

Система векторов, которая не является линейно зависимой, называется линейно независимой. Но последнее определение лучше сформулировать по другому.

        Определение 10.15   Система векторов   называется линейно независимой, если равенство   возможно только при   .         

Кто плохо понял два последних определения, может получить дополнительные объяснения здесь.

        Предложение 10.6   Система векторов   линейно зависима тогда и только тогда, когда один из векторов системы является линейной комбинацией остальных векторов этой системы.

        Доказательство.     Пусть система векторов линейно зависима. Тогда существует такой набор коэффициентов   , что   , причем хотя бы один коэффициент отличен от нуля. Предположим, что   . Тогда

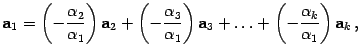
то есть   является линейной комбинацией остальных векторов системы.

Пусть один из векторов системы является линейной комбинацией остальных векторов. Предположим, что это вектор   , то есть   . Очевидно, что   . Получили, что линейная комбинация векторов системы равна нулю, причем один из коэффициентов отличен от нуля (равен   ).      

        Предложение 10.7   Если система векторов содержит линейно зависимую подсистему, то вся система линейно зависима.

        Доказательство.    

Пусть в системе векторов   подсистема   ,   , является линейно зависимой, то есть   , и хотя бы один коэффициент отличен от нуля. Тогда составим линейную комбинацию   . Очевидно, что эта линейная комбинация равна нулю, и что среди коэффициентов есть ненулевой.      

Упражнение10.4.1. Докажите, что если система векторов линейно независимая, то любая ее подсистема линейно независимая.     

        Предложение 10.8   Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.

        Доказательство.     Пусть система состоит из вектора   . Линейная комбинация имеет вид   . Если   , то   , то есть система линейно зависима. Если   и   , то   .      

        Предложение 10.9   Система, состоящая из двух векторов, линейно зависима тогда и только тогда, когда эти векторы коллинеарны.

        

Доказательство этого предложения предоставляется читателю. Оно аналогично доказательству следующего предложения.

        Предложение 10.10   Система из трех векторов линейно зависима тогда и только тогда, когда эти векторы компланарны.

        Доказательство.     Пусть векторы    -- компланарные. Если    -- коллинеарные, то в силу предыдущего предложения они образуют линейно зависимую подсистему системы   . По  предложению 10.7 система    -- линейно зависима. Если векторы   -- неколлинеарные, то по  предложению 10.2   является линейной комбинацией векторов   и по  предложению 10.6 система векторов    -- линейно зависимая.

Пусть система векторов линейно зависима. По  предложению 10.6 один вектор, скажем   , является линейной комбинацией других векторов,   и   ,   . Правая часть последнего равенства лежит в плоскости, в которой лежат векторы   . Поэтому вектор   лежит в одной плоскости с векторами   , то есть векторы    -- компланарные.      

        Предложение 10.11   Четыре вектора всегда образуют линейно зависимую систему.

        Доказательство.     Если первые три вектора являются компланарными, то они образуют линейно зависимую подсистему ( предложение 10.10). Следовательно, вся система линейно зависима ( предложение 10.7). Если первые три вектора -- некомпланарные, то четвертый является их линейной комбинацией ( предложение 10.3). По  предложению 10.6 система является линейно зависимой.      

На основании сказанного дадим другое определение базиса, которое является более распространенным, чем  определение 10.12.

        Определение 10.16   Базисом векторного пространства   называется такая упорядоченная линейно независимая система векторов, что любой вектор пространства   раскладывается по векторам этой системы.         

Из  предложений 10.8 – 10.11 следует, что это определение эквивалентно определению 10.12.

9.НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ КОЛЛИНЕАРНОСТИ И КОМПЛАНАРНОСТИ ВЕКТОРОВ.

Необходимое и достаточное условие компланарности векторов  a = ( x, y, z ),  b = ( u, v, w )  и  c = ( p, q, r ) :  

П р и м е р .   Даны векторы:  a = ( 1, 2, 3 ) и  b = ( – 2 , 0 ,4 ).

                       Вычислить их скалярное и векторное произведения и угол

                       между этими векторами.

 

Р е ш е н и е . Используя соответствующие формулы (см. выше), получим:

                      a).скалярное произведение:

                   

                                  ( a , b ) = 1 · ( – 2 ) + 2 · 0 + 3 · 4 = 10 ;

                                    б).векторное произведение:             

                                  

Необходимое и достаточное условие компланарности векторов  a = ( x, y, z ),  b = ( u, v, w )  и  c = ( p, q, r ) :  

П р и м е р .   Даны векторы:  a = ( 1, 2, 3 ) и  b = ( – 2 , 0 ,4 ).

                       Вычислить их скалярное и векторное произведения и угол

                       между этими векторами.

 

Р е ш е н и е . Используя соответствующие формулы (см. выше), получим:

                      a).скалярное произведение:

                   

                                  ( a , b ) = 1 · ( – 2 ) + 2 · 0 + 3 · 4 = 10 ;

                                    б).векторное произведение: