27. Предел функции в точке.
Пусть функция f(x) определена в некоторой проколотой окрестности точки x0 .
Число A называется пределом функции f(x) при x → x0 (или в точке x0), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < |x − x0| < δ, справедливо неравенство |f(x) − A| < ε, т.е.
lim |
x → x0 |
f(x) = A ε > 0 δ > 0 : 0 < |x − x0| < δ |f(x) − A| < ε.
Используем понятие окрестности и учтем, что
0 < |x − x0| < δ x
· |
O |
δ (x0 ) и |f(x) − A| < ε f(x) Oε (A).
(Точка над символом окрестности указывает, что это проколотая окрестность.)
Теперь определение предела функции в точке можно представить в виде
|
f(x) = A ε > 0 δ > 0 : x
δ (x0 ) f(x) Oε (A). |
|
Еше проще:
|
f(x) = A O (A)
(x0) : x
(x0) f(x) O (A). |
|
Геометрический смысл того, что x
· |
O |
(x0) f(x) O (A) поясняет рис.1
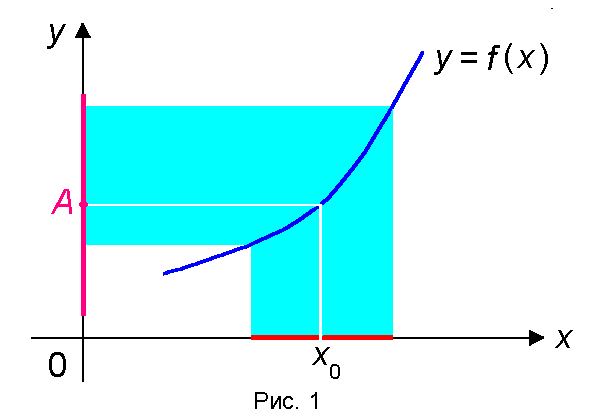
На этом рисунке проколотая окрестность
· |
O |
(x0) точки x0 изображена красным отрезком на оси OX из которого исключена точка x0. Окрестность O (A) точки A изображена розовым отрезком на оси OY. Очевидно, что образ окрестности
· |
O |
(x0) при отображении y = f(x) содержится в O (A).
Пределы суммы, произведения и частного двух функций
Теорема 1. Если существуют
lim |
x → x0 |
f(x) = A и
lim |
x → x0 |
g(x ) = B, то существуют пределы
[f(x) ± g(x) ] = A ± B;
[ f(x) · g(x) ] = A · B;
=
, (B ≠ 0). |
Доказательство приведено в книге Я.С. Бугрова и С.М. Никольского “Дифференциальное и интегральное исчисление”. М.: ФИЗМАТЛИТ, 1980. Стр. 84.
Теорема 2 (о переходе к пределу в неравенстве). Если x
· |
O |
(x0) f(x) ≤ g(x) и существуют пределы
lim |
x → x0 |
f(x) и
lim |
x → x0 |
g(x) , то
lim |
x → x0 |
f(x) ≤
lim |
x → x0 |
g(x) .
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 44.
Замечание. Строгое неравенство f(x)<g(x) при переходе к пределу может перейти в равенство.
Теорема 3 (о пределе промежуточной функции). Если x
· |
O |
(x0) u(x) ≤ f(x) ≤ v(x) и
lim |
x → x0 |
u(x) =
lim |
x → x0 |
v (x) = A, то
lim |
x → x0 |
f(x) = A.
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 45.
Односторонние пределы
Пусть функция f(x) определена на интервале (x0, x1).
Число A называется пределом функции f(x) справа, в точке x0 если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых x0 < x < x0 + δ , справедливо неравенство | f(x) − A | < ε, т.е.
|
f(x) = A ε > 0 δ > 0 : x0 < x < x0 + δ | f(x) − A | < ε. |
|
Предел функции f(x) в точке x0 справа обозначается символом f(x0 + 0)
Число A называется пределом функции f(x) слева, в точке x1 если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых x1 − δ < x < x1 , справедливо неравенство | f(x) − A | < ε, т.е.
|
f(x) = A ε > 0 δ > 0 : x1 − δ < x < x1 | f(x) − A | < ε. |
|
Предел функции f(x) в точке x1 слева обозначается символом f(x1 − 0)
Теорема 4. Для того чтобы существовал предел
lim |
x → a |
f(x) , равный A, необходимо и достаточно, чтобы существовали и были равны A оба односторонних предела
lim |
x → a − 0 |
f(x) и
lim |
x → a + 0 |
f(x) .
Функция f(x) называется ограниченной в точке x0, если существуют число M > 0 и окрестность O(x0), такие что x O(x0) | f(x) | < M .
Теорема 5. Если функция f(x) определена в некоторой окрестности точки x0 и имеет в точке x0 односторонние пределы, то она ограничена в этой точке.
Доказательство приведено в книге Я.С. Бугрова и С.М. Никольского “Дифференциальное и интегральное исчисление”. М.: ФИЗМАТЛИТ, 2002. Стр. 81.
Функция f(x) называется бесконечно большой при x → x0, если
|
M > 0
(x0) : x
(x0) | f(x) | > M. |
|
В этом случае принято говорить, что предел функции бесконечен, и записывать этот факт в виде
|
f(x) = ∞. |
|
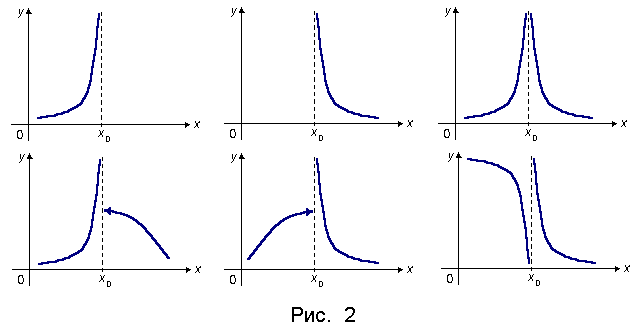
Прямая x = x0 называется вертикальной асимптотой графика функции y = f(x), если хотя бы один из односторонних пределов f(x0 + 0) и f( x0 − 0) равен + ∞ или −∞.
Некоторые (не не все!) примеры поведения графика функции y = f(x) вблизи вертикальной асимптоты x = x0 изображены на рис. 2.
