
- •1Матрицы.Действия с матрицами
- •3.Миноры и алгебраические дополнения.Обратная матрица
- •1) Если система (2.3) имеет единственное решение, определяемое по формулам: .
- •7. Векторы. Действия с векторам. Коллиниарность векторов
- •8.Линейная зависимость векторов
- •10. Понятие базис.Разложение вектора по базису.
- •11.Декартовая система координат. Направление косинуса вектора.
- •12. Скалярное произведение векторов. Необходимое и достаточное условие.
- •13.Векторное произведение. Необходимое и достаточное условие векторов.
- •14. Смешанное произведение векторов. Компланарность векторов.
- •15. Плоскость в пространстве. Основные уравнения плоскости.
- •16. Расстояние от произвольной точки до плоскости. Условия перпендикулярности и параллельности прямых на плоскости. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.
- •17. Прямая в пространстве. Различные уравнения прямой
- •18. Переход от общего уравнения прямой к кононическому.
- •19. Взаимное расположение прямой в пространстве
- •20. Прямая на плоскости. Различные формы уравнений прямой на плоскости.
- •21. Расстояние от произвольной точки до прямой на плоскости. Условия параллельности и перпендикулярности прямых на плоскости.
- •22. Каноническое уравнение прямых второго порядка. Элипс, гипербола, парабола
- •23. Преобразование координат на плоскости. Приведение общего уравнения кривой второго порядка у каноническому виду
- •24.Множества. Действительные числа. Логически символы. Окрестность точки
- •25. Числовые последовательности. Предел числовой последовательности. Теорема вейерштрасса.
- •26. Определение функции. Способы задания функции. Основные характеристики функций. Элементарные функции.
- •27. Предел функции в точке.
- •28.Предел функции при X→∞. Односторонние пределы.
- •29. Бесконечно малые и бесконечно большие функции. Свойства бесконечно малые и бесконечно большие функций.
- •30. Связь бесконечно малых и бесконечно больших. Их свойства.
- •31. Теорема о связи между функцией, ее пределом и бесконечно малой величиной.
- •32. Признак существования предела функции. Первый замечательный предел. Первый замечательный предел
- •33. Основные свойства пределов функций. Основные типы неопределенностей.
- •Основные неопределенности пределов и их раскрытие.
- •34. Второй замечательный предел. Три формы записи второго замечательного предела.
- •35. Эквивалентные бесконечно малые. Сравнение бесконечно малых.
- •36. Непрерывность функции в точке. Три определения непрерывности.
- •37. Точки разрыва функции и их классификация
- •38. Основные теоремы о непрерывных функциях.
- •39. Свойства функций непрерывных на отрезке. Геометрическая интерпретация этих свойств.
18. Переход от общего уравнения прямой к кононическому.
Переход от общих уравнений прямой к каноническим или параметрическим уравнениям
|
Для того, чтобы от общих уравнений
каноническим или параметрическим уравнениям прямой,
требуется
найти направляющий вектор
прямой
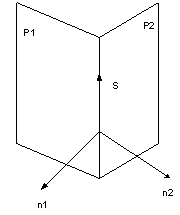
и координаты любой точки принадлежащей ей. Направляющий вектор прямой ортогонален
нормалям
к
обеим плоскостям, следовательно, коллинеарен их векторному произведению
направляющего
вектора можно выбрать или любой вектор с пропорциональными координатами. Чтобы найти точку, лежащую на данной прямой, можно задать одну ее координату произвольно, а две остальные
найти из уравнений , выбрав их так, чтобы определитель из их коэффициентов не равнялся нулю. |
Пример.
Составить канонические и параметрические
уравнения прямой ![]() .
.
Решение.
По условию ![]() ,
, ![]() тогда
тогда ![]() .
Следовательно, направляющим вектором
прямой можно считать вектор
.
Следовательно, направляющим вектором
прямой можно считать вектор ![]() .
.
Будем
искать точку на прямой с координатой ![]() .
Для координат
.
Для координат ![]() и
и ![]() получим
систему уравнений
получим
систему уравнений ![]() ,
откуда
,
откуда ![]() ,
, ![]() .
Теперь можно составить канонические
уравнения прямой:
.
Теперь можно составить канонические
уравнения прямой:
![]() .
.
Параметрические уравнения той же прямой имеют вид:
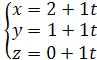 или
или 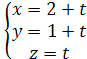 .
.
Пример.
Привести общие уравнения прямой ![]() к
каноническому виду.
к
каноническому виду.
Решение.
Найдём точку, лежащую на прямой. Для
этого выберем произвольно одну из
координат, например, ![]() и
решив систему уравнений
и
решив систему уравнений ![]() найдем
найдем ![]() .
.
Нормальные
векторы плоскостей, определяющих прямую,
имеют координаты ![]() ,
, ![]() .
Поэтому направляющий вектор прямой
будет
.
Поэтому направляющий вектор прямой
будет ![]() .
Следовательно,
.
Следовательно, ![]() .
.
Замечание. Если какая-либо из координат направляющего вектора равна 0, то предполагается, что для любой точки прямой числитель соответствующей дроби в канонических уравнениях тоже равен 0.
Пусть
прямая перпендикулярна одной из
координатных осей, например оси ![]() .
Тогда направляющий вектор
прямой
перпендикулярен
.
Тогда направляющий вектор
прямой
перпендикулярен
,
следовательно, ![]() и
параметрические уравнения прямой примут
вид
и
параметрические уравнения прямой примут
вид 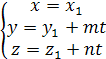 .
Исключаяиз уравнений параметр t,
получим уравнения прямой в виде
.
Исключаяиз уравнений параметр t,
получим уравнения прямой в виде 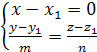 .
.
Однако,
и в этом случае, формально записывают
канонические уравнения прямой в виде ![]() .
.
Таким образом, если в знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Аналогично,
каноническим уравнениям ![]() соответствует
прямая перпендикулярная осям
и
соответствует
прямая перпендикулярная осям
и ![]() или
параллельная оси
или
параллельная оси ![]() .
.
Пример.
Записать уравнение прямой ![]() в параметрическом виде.
в параметрическом виде.
Решение.
Обозначим ![]() ,
отсюда
,
отсюда 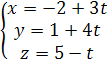
Пример.
Составить канонические и параметрические
уравнения прямой, проходящей через
точку ![]() параллельно
вектору
параллельно
вектору ![]() .
.
Решение.
Канонические уравнения: ![]() или
или ![]() .
.
Параметрические
уравнения: 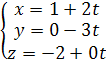 или
или 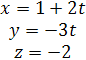 .
.
19. Взаимное расположение прямой в пространстве
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.
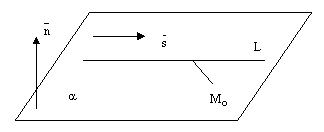
рис.6.
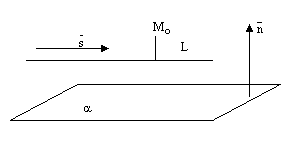
рис.7.
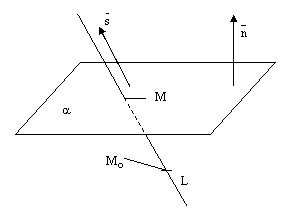
рис.8.
Теорема.
Пусть плоскость ![]() задана
общим уравнением
задана
общим уравнением
![]() ,
,
а прямая L задана каноническими уравнениями
![]()
или параметрическими уравнениями
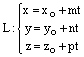 ,
, ![]() ,
,
в
которых ![]() – координаты нормального вектора плоскости
,
– координаты нормального вектора плоскости
, ![]() – координаты произвольной
фиксированной точки прямой L,
– координаты произвольной
фиксированной точки прямой L, ![]() –
–
координаты направляющего вектора прямой L. Тогда:
1)
если ![]() ,
то прямая L пересекает плоскость
в
точке,координаты которой
,
то прямая L пересекает плоскость
в
точке,координаты которой ![]() можно
найти из системы уравнений
можно
найти из системы уравнений
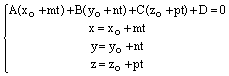 ;
(7)
;
(7)
2)
если ![]() и
и ![]() ,
то прямая лежит на плоскости;
,
то прямая лежит на плоскости;
3)
если
и ![]() ,
то прямая параллельна плоскости.
,
то прямая параллельна плоскости.
Доказательство.
Условие ![]() говорит
о том, что вектроры
говорит
о том, что вектроры ![]() и
и ![]() не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координаты точки
М удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальныеуравнения системы,
находим координаты искомой
точки.
не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координаты точки
М удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальныеуравнения системы,
находим координаты искомой
точки.
Если ![]() ,
то это означает, что
,
то это означает, что ![]() .
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
икоординаты любой
точки прямой удовлетворяют уравнению
плоскости. Поэтому достаточно проверить,
лежит ли на плоскости точка
.
Если
,
то точка
.
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
икоординаты любой
точки прямой удовлетворяют уравнению
плоскости. Поэтому достаточно проверить,
лежит ли на плоскости точка
.
Если
,
то точка ![]() –
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
–
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
Если , а , то точка напрямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.
Теорема доказана.

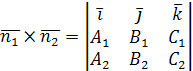 .
Поэтому в качестве
.
Поэтому в качестве