
- •Теплопроводность, основной закон теплопроводности.
- •Теплопередача через однородную цилиндрическую стенку.
- •Теплопроводность плоской стенки.
- •4 Теплопередача через многослойную цилиндрическую стенку.
- •Теплопроводность цилиндрической стенки.
- •Теплопередача через ребристые поверхности.
- •Теплопроводность шаровой стенки и тел неправильной формы.
- •Теплопередача через жидкостные и газовые прослойки.
- •Теплопроводность тел с внутренними источниками теплоты.
- •Интенсификация процессов теплопередачи.
- •Конвективный теплообмен, общие понятия и определения.
- •Тепловая изоляция, её виды и назначение.
- •Дифференциальное уравнение конвективного теплообмена.
- •Условия рационального выбора материала для тепловой изоляции трубопроводов.
- •Основы теории подобия.
- •Процессы массообмена, общие положения и расчетные зависимости.
- •17 Подобие процессов конвективного теплообмена
Дифференциальное уравнение конвективного теплообмена.
Т.к. теплоотдача опр. не только тепловыми, но и гидродинамич. явл., то совокупность этих явл. опис. сист. дифф.ур-й, в кот. входят ур-е теплопроводности, ур-е движения и ур-е сплошности.
1. Ур-е теплопроводности:
 Чтобы
найти коэфф. теплоотдачи надо знать
темп.градиент и распред. темп. в жидк.
Дифф.ур-е теплопроводности вывод.на
основе з-на сохранения энергии. Выд.
элемен. параллелепипед с гранями dx,
dy,
dz,
и. считая физич. парам. постоянными,
запишем ур-е теплового баланса. Если
измен.давл. пренебречь, то согласно
первому з-ну темрод: к-во подведенной
теплоты = измен.энтальпии тела. Согл.
з-ну Фурье: к-во теплоты, проход. за время
в напр. Ох через грань АВСD:
Чтобы
найти коэфф. теплоотдачи надо знать
темп.градиент и распред. темп. в жидк.
Дифф.ур-е теплопроводности вывод.на
основе з-на сохранения энергии. Выд.
элемен. параллелепипед с гранями dx,
dy,
dz,
и. считая физич. парам. постоянными,
запишем ур-е теплового баланса. Если
измен.давл. пренебречь, то согласно
первому з-ну темрод: к-во подведенной
теплоты = измен.энтальпии тела. Согл.
з-ну Фурье: к-во теплоты, проход. за время
в напр. Ох через грань АВСD:
 ,
а через грань EFGH,
имеющ. темп.
,
а через грань EFGH,
имеющ. темп. :
:
 .
.
 .
Аналогично для Оу и Оz.
Общее к-во теплоты:
.
Аналогично для Оу и Оz.
Общее к-во теплоты:
 .Темп.
измен. на величину
.Темп.
измен. на величину
 ,
а энтальпия:
,
а энтальпия:
 .
.
 - дифф.ур-е теплопроводности Фурье-Кирхгофа:
устанавливает связь между временными
и пространственными изм.темп. в любой
точке движущ. среды; а –
коэфф.температуропроводности и
- дифф.ур-е теплопроводности Фурье-Кирхгофа:
устанавливает связь между временными
и пространственными изм.темп. в любой
точке движущ. среды; а –
коэфф.температуропроводности и
 - оператор Лапласа.
- оператор Лапласа.
2. Ур-е движения:
 Темп.поле
в движущ.жидк. зависит от распред.
скоростей. Описывается дифф.ур-ем движ.,
вывод кот. основан на на 2 з-не Ньютона:
сила равна массе, умноженной на ускорение.
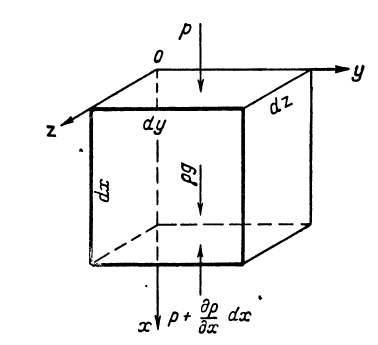
Выд. в потоке движущ. жидк.
элемент.параллелепипед с ребрами dx,
dy,
dz.
На выд.объеме действуют три силы: сила
тяжести, сила давления и сила трения.
а) сила тяжести приложена в центре
тяжести элемента объемом dV.
Её проекция на ось х= произв. проекции
ускорения свободного падения на массу:
Темп.поле
в движущ.жидк. зависит от распред.
скоростей. Описывается дифф.ур-ем движ.,
вывод кот. основан на на 2 з-не Ньютона:
сила равна массе, умноженной на ускорение.
Выд. в потоке движущ. жидк.
элемент.параллелепипед с ребрами dx,
dy,
dz.
На выд.объеме действуют три силы: сила
тяжести, сила давления и сила трения.
а) сила тяжести приложена в центре
тяжести элемента объемом dV.
Её проекция на ось х= произв. проекции
ускорения свободного падения на массу:
 .
б) равнодейств. сил давления опред. на
основе след.соображений: если на верхней
грани элемента давл. жидк. = Р, то на
площадку dydz
действует сила Р dydz.
На нижней грани давл.жидк. =
.
б) равнодейств. сил давления опред. на
основе след.соображений: если на верхней
грани элемента давл. жидк. = Р, то на
площадку dydz
действует сила Р dydz.
На нижней грани давл.жидк. =
 ,
и на эту грань действ. сила
,
и на эту грань действ. сила
 .
Здесь «-» указ., что эта сила действует
против напр. оси х. Равнод. сил = их
алгебраической сумме:
.
Здесь «-» указ., что эта сила действует
против напр. оси х. Равнод. сил = их
алгебраической сумме:
 .
в) при движении в реальной жидк. возникает
сила трения:
.
в) при движении в реальной жидк. возникает
сила трения:
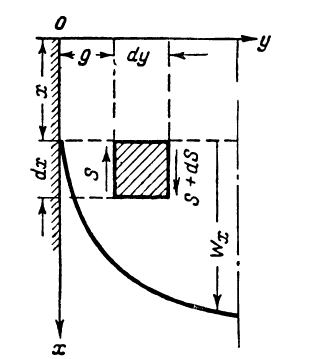 выр.
может быть установлено из рассм. плоского
ламинарного потока, в кот. скорость
изменяется лишь в напр. оси у. В этом
случае сила трения возн. только на
бок.гранях элемента. Около левой грани
скорость движ.частицы меньше, чем в
самом элементе. Около правой – больше.
Равнодействующая сил:
выр.
может быть установлено из рассм. плоского
ламинарного потока, в кот. скорость
изменяется лишь в напр. оси у. В этом
случае сила трения возн. только на
бок.гранях элемента. Около левой грани
скорость движ.частицы меньше, чем в
самом элементе. Около правой – больше.
Равнодействующая сил:
 ,
S
– касательная сила трения на 1 поверхности,
согласно з-ну Ньютона:
,
S
– касательная сила трения на 1 поверхности,
согласно з-ну Ньютона:
 .
Принимая
.
Принимая
 :
:
 .
Когда
.
Когда
 изм.
по всем 3 напр. проекция равнод.сил трения
на ось х:
изм.
по всем 3 напр. проекция равнод.сил трения
на ось х:
 .
Согласно 2 з-ну механики равнод. =
произведению массы элемента на ускорение:
.
Согласно 2 з-ну механики равнод. =
произведению массы элемента на ускорение:
 .
.
 все компоненты имеют размерность силы,
отнесенной к 1 объема (Н/м3). Аналогично
для осей у и z.
Эти ур-я и есть дифф.ур-я движ. несжимаемой
вязкой жидкости – ур-е Навье-Стокса:
справедливо как для ламинарного, так и
турбулентного.
все компоненты имеют размерность силы,
отнесенной к 1 объема (Н/м3). Аналогично
для осей у и z.
Эти ур-я и есть дифф.ур-я движ. несжимаемой
вязкой жидкости – ур-е Навье-Стокса:
справедливо как для ламинарного, так и
турбулентного.
3. Ур-е сплошности:
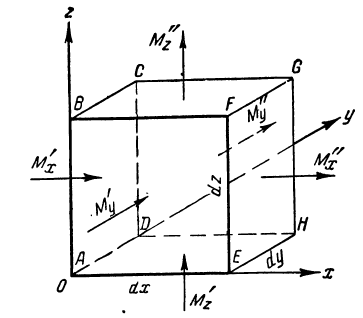 т.к.
в ур-е движения появилась новая
неизвестная Р, то число неизв. больше
числа ур-й, т.е. система оказалась
незамкнутой. Чтобы получить замкнутую
систему, необходимо к имеющ.ур-ям присоед.
ещё 1 – ур-е сплошности, кот. вывод. на
основе з-на сохранения массы. Выд. в
потоке движ. жидк. элемент. параллел. со
стор. dx,
dy,
dz
и подсч. массу жидк, протекающей через
него за время тау. В направлении оси х
через грань АВСD
втекает масса жидкости:
т.к.
в ур-е движения появилась новая
неизвестная Р, то число неизв. больше
числа ур-й, т.е. система оказалась
незамкнутой. Чтобы получить замкнутую
систему, необходимо к имеющ.ур-ям присоед.
ещё 1 – ур-е сплошности, кот. вывод. на
основе з-на сохранения массы. Выд. в
потоке движ. жидк. элемент. параллел. со
стор. dx,
dy,
dz
и подсч. массу жидк, протекающей через
него за время тау. В направлении оси х
через грань АВСD
втекает масса жидкости:
 .
Через противоположную грань EFGH
вытекает:
.
Через противоположную грань EFGH
вытекает:
 .
Изменение массы жидкости, вытек. из
объема по оси х:
.
Изменение массы жидкости, вытек. из
объема по оси х:
 .
Аналогично для у и z.
Полный избыток массы, вытекающей жидк.:
.
Аналогично для у и z.
Полный избыток массы, вытекающей жидк.:
 .Этот
избыток обусловлен уменьшением плотности
жидкости в объеме dV
и = изменению массы данного объема во
времени:
.Этот
избыток обусловлен уменьшением плотности
жидкости в объеме dV
и = изменению массы данного объема во
времени:
 .
.
 - дифф.ур-е сплошности или непрерывности
в самом общем виде.
- дифф.ур-е сплошности или непрерывности
в самом общем виде.
4. Краевые условия. Сист.дифф. ур-й для конвективного теплообмена охватывает бесчисл. множество проц. теплоотдачи. Чтобы ограничить задачу, из бесчисленного множества выд.рассм. процесс и определить его однозначно, т.е дать полное матем. описание, к сист дифф.ур-й необходимо присоед. матем. описание всех частных особен., кот. наз. условиями однозначности или краевыми. Усл.однозначности: геометрические усл (хар-ют форму и размеры сист., в кот. протекает процесс); физические (хар-ют физ.св-ва среды и тела); граничные (хар-ют особен. протекания процесса на границах тела); временные (хар-ют особен. протекания процесса во времени).
