5. Теплопроводность цилиндрической стенки.

Линейная плотность теплового потока , Вт/м, проходящего через цилиндрическую стенку от греющей жидкости внутри трубы к нагреваемой – снаружи: теплоотдача на внутр.поверхн. ; распространение теплоты в стенке теплопроводностью: ; теплоотдача на внешней поверхности стенки к нагреваемой жидкости: .

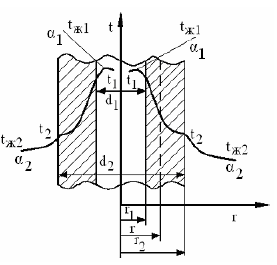Линейная плотность теплового потока: . наз. линейным коэфф.теплопередачи для трубы, Вт/м К. Ур-е теплопередачи для цилиндрической стенки: . Линейный коэфф.теплопередачи численно равен к-ву теплоты, проход. в 1 секунду через цилиндрическую поверхность длиной 1м при разности температур между жидк. 1К. Величина, обратная линейному коэфф. теплопередачи: линейным термическим сопротивлением теплопередачи через цилиндрическую стенку. Величины и наз. частными сопротивлениями теплоотдачи на соответ. поверхн., или поверхностными сопротивлениями. Т.о., полное линейное термическое сопротивление теплопередачи явл. суммой частных сопротивлений теплоотдачи и линейного сопротивления.

5. Теплопередача через ребристые поверхности.

Теплопередачей называется теплообмен между двумя жидкостями - теплоносителями, разделенными стенкой.

Необходимо найти тепловой поток через плоскую ребристую стенку безграничных размеров. Стенка оребрена со стороны меньшего коэффициента теплоотдачи. Заданы постоянные значения коэффициентов теплоотдачи на неоребренной поверхности стенки  ₁, гладкой части оребренной поверхности  _с и на поверхности ребер  _р. Заданы геометрические размеры ребер и температуры теплоносителей t_F1 и t_F2.

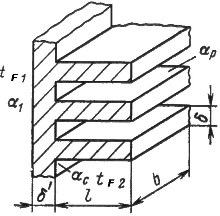Поскольку для ребра Ь>>δ, то полагаем, что периметр поперечного сечения реберu=2Ь. Площадь поперечного сечения ребра f=Ьδ. Следовательно,  . . Подставив выражение для m в уравнение, умножив и разделив на 2l,получим предыдущее выражение, где   _рδ/λ=Bi - безразмерный комплекс, называемый числом Био. Число Bi является важной характеристикой процесса теплопроводности. Оно представляет собой отношение внутреннего термического сопротивления теплопроводности к внешнему термическому сопротивлению теплоотдачи: . Окончательное уравнение для теплового потока с поверхности ребра можно записать в виде . . .при заданных геометрических размерах ребра последнее возможно, если λ стремиться к бесконечности, т. е. Biстремиться к нулю). Величина Е называется коэффициентом эффективности ребра. Тепловой поток Q_c,Вт, отдаваемый гладкой частью оребренной поверхности. . или . . .

Величина  _пр, входящая в уравнение (2.87), называется приведенным коэффициентом теплоотдачи. Это такой усредненный коэффициент теплоотдачи ребристой стенки, который учитывает теплоотдачу поверхности ребра, поверхности гладкой стенки и эффективность работы ребра. Для передачи теплоты через ребристую стенку можно записать систему уравнений: . Получаем , , - Если тепловой потока отнести к единице оребренной поверхности стенки, где - коэфф.теплопередачи через ребристую стенку при отнесении теплового потока к оребренной поверхности. Если тепловой поток отнести к неоребренной поверхности стенки, то . . к₁ – коэфф теплопередачи при отнесении теплового потока к неоребренной поверхности стенки. Отношение оребренной поверхности к гладкой наз. коэфф. оребрения. Влияние оребрения на коэффициент теплопередачи можно показать на следующем примере. Пусть  ₁=1000 и  ₂=20Вт/(м²К). Предположим, что δ'/λ мало и им можно пренебречь, тогда . Для плоской поверхности (коэффициент оребрения F_p.c/F₁ равен единице) получим: .