21. Барометрическая формула. Распределение Больцмана. Распределение Больцмана

Распределение Больцмана — распределение вероятностей различных энергетических состояний идеальной термодинамической системы (идеальный газ атомов или молекул) в условиях термодинамического равновесия; открыто Л. Больцманом в 1868—1871.

Согласно распределению Больцмана среднее число частиц с полной энергией   равно

где   — кратность состояния частицы с энергией   — число возможных состояний частицы с энергией  . Постоянная   находится из условия, что сумма   по всем возможным значениям   равна заданному полному числу частиц   в системе (условие нормировки):

В случае, когда движение частиц подчиняется классической механике, энергию   можно считать состоящей из

• кинетической энергии 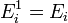 (кин) частицы (молекулы или атома),

• внутренней энергии 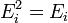 (вн) (например, энергии возбуждения электронов) и

• потенциальной энергии 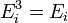 (пот) во внешнем поле, зависящей от положения частицы в пространстве:

Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести.

Для идеального газа, имеющего постоянную температуру   и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения   одинаково), барометрическая формула имеет следующий вид:

где   — давление газа в слое, расположенном на высоте  ,   — давление на нулевом уровне ( ),   — молярная масса газа,   — универсальная газовая постоянная,   —абсолютная температура. Из барометрической формулы следует, что концентрация молекул   (или плотность газа) убывает с высотой по тому же закону:

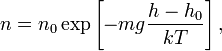
где   — масса молекулы газа,   — постоянная Больцмана.

21. Введение в термодинамику. Термодинамическая система, процесс, параметры. Число степеней свободы. Закон Больцмана о равнораспределении энергии по степеням свободы молекулы. Первое начало термодинамики. Работа газа при изменении объема.

    Термодинамические системы

В термодинамике изучаются физические системы, состоящие из большого числа частиц и находящиеся в состоянии термодинамического равновесия или близком к нему. Такие системы называются термодинамическими системами. Это понятие в общем случае достаточно сложно определить строго, поэтому используется описательное определение, в котором термодинамической системой называется макроскопическая система, которая каким-то образом (например, с помощью реальной или воображаемой оболочки) выделена из окружающей среды и способна взаимодействовать с ней. Если оболочка не допускает обмен ни веществом, ни энергией между системой и окружающей средой, то такая оболочка называется адиабатической, а соответствующая система - изолированной или замкнутой. Системы, у которых оболочка не препятствует обмену веществом и энергией, называются открытыми.

Термодинамические параметры

Термодинамика не рассматривает особенности строения тел на молекулярном уровне. Равновесные состояния термодинамических систем могут быть описаны с помощью небольшого числамакроскопических параметров, таких как температура, давление, плотность, концентрации компонентов и т. д., которые могут быть измерены макроскопическими приборами. Описанное таким образом состояние называется макроскопическим состоянием, и законы термодинамики позволяют установить связь между макроскопическими параметрами. Если параметр имеет одно и то же значение, не зависящее от размера любой выделенной части равновесной системы, то он называется неаддитивным или интенсивным, если же значение параметра пропорционально размеру части системы, то он называется аддитивным или экстенсивным^[9]. Давление и температура — неаддитивные параметры, а внутренняя энергия и энтропия — аддитивные параметры.

Макроскопические параметры могут подразделяться на внутренние, характеризующие состояние системы как таковой, и внешние, описывающие взаимодействие системы с окружающей средой и силовыми полями, воздействующими на систему, однако это разделение достаточно условно. Так, если газ заключен в сосуд с подвижными стенками и его объём определяется положением стенок, то объём является внешним параметром, а давление газа зависит от скоростей теплового движения молекул и является внутренним параметром. Напротив, если задаётся внешнее давление, то его можно считать внешним параметром, а объём газа — внутренним параметром. Постулируется, что в состоянии термодинамического равновесия каждый внутренний параметр может быть выражен через внешние параметры и температуру системы. Такая функциональная связь называется обобщённым уравнением состояния системы^[10].