Среднее число столкновений и средняя длина свободного пробега молекул

средняя длина свободного пробега   - это среднее расстояние, которое проходит молекула от столкновения до столкновения.

движущаяся со средней скоростью молекула в течении одной секунды столкнется со всеми молекулами, центры которых находятся в объеме ограниченном цилиндром с радиусом 2r и длиной   , т.е.

.

Если концентрация молекул n , то внутри рассмотренного цилиндра находится число молекул, равное

Это число   и определяет среднее число соударений за единицу времени.

 В действительности все молекулы движутся, и возможность соударения двух частиц зависит от их относительной скорости.

Средний путь, проходимый молекулой за единицу времени, численно равен   . Поэтому средняя длина свободного пробега равна   или

средняя длина свободного пробега   не зависит от температуры газа, т.к. с ростом температуры одновременно возрастают и   , и   .

Среднее расстояние между центрами молекул, взаимодействующих, как при упругом ударе, называют эффективным диаметром   .

Уравнение Фурье

Уравнение теплопроводности — важное уравнение в частных производных, которое описывает распространение тепла в заданной области пространства во времени.

Для функции u(x,y,z,t) трёх пространственных переменных (x,y,z) и времени t, уравнение теплопроводности имеет вид

,

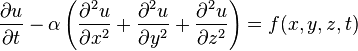где   — функция тепловых источников.

Для произвольной системы координат:

где α — положительная константа, а Δ или ∇² — оператор Лапласа.

21. Молекулярно-кинетическая теория идеальных газов. Понятие идеального газа.Законы Бойля-Мариотта, Гей-люссака, Авогадро и Дальтона. Молекулярно-кинетическая теория идеальных газов

Молекулярно-кинетическая теория (МКТ) устанавливает связи между макро- и микропараметрами идеального газа. Основное уравнение МКТ выражает выражает связь давления газа со средней кинетической энергией поступательного движения молекул. Давление газа на стенки сосуда является результатом многочисленных ударов молекул. При каждом ударе стенка получает силовой импульс, величина которого зависит от скорости молекул и, следовательно, от энергии их движения. При огромном числе ударов создается постоянное давление газа на стенку. Число ударов зависит от концентрации молекул n. Таким образом, можно ожидать, что давление газа связано с концентрацией молекул и с энергией их движения. Получим основное уравнение МКТ.

	расстояния между молекулами велики по сравнению с их размерами;
	взаимодействие между молекулами на расстоянии отсутствует;
	при столкновениях молекул действуют большие силы отталкивания;
	время столкновения много меньше времени свободного движения между столкновениями.

,            (11) где n   –концентрация молекул.

Это уравнение называется основным уравнением молекулярно-кинетической теории идеального газа.

Авогадро вывел закон, что в равных объемах газа содержится одинаковое коли-

чество молекул. Учитывая, что в одном моле газа содержится NA молекул, мо-

жем получить связь между постоянной Больцмана и универсальной газовой по-

стоянной:

R A = kN