Реальные газы. Силы и потенциальная энергия межмолекулярного взаимодействия. Уравнения Ван-дер-Ваальса. Анализ изотерм Ван-дер-Ваальса. Сжижение газов.
Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева. Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём.
Межмолекулярное взаимодействие — взаимодействие между электрически нейтральными молекулами или атомами.
Силы межмолекулярных взаимодействий подразделяются на силы притяжения и силы отталкивания. Оба типа сил действуют одновременно.
Силы межмолекулярного взаимодействия— консервативные силы. Они обуславливают наличие взаимной потенциальной энергии.
Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.
Для одного моля газа Ван-дер-Ваальса оно имеет вид:
где
— давление,
— молярный объём,
— абсолютная температура,
— универсальная газовая постоянная.
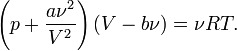
где
— объём,
Сжижение газов - переход вещества из газообразного состояния в жидкое. Оно достигается охлаждением их ниже критической температуры (Тк) и последующей конденсацией в результате отвода теплоты парообразования (конденсации).
Фазовые переходы. Фазовые переходы 1 и 2-го рода. Уравнение Клапейрона-Клаузиуса. Диаграмма состояний. Тройная точка.
Фазовый переход – переход вещества из одной фазы в другую при изменении внешних условий – температуры, давления.
Фазовые переходы второго рода — фазовые переходы, при которых вторые производные термодинамических потенциалов по давлению и температуре изменяются скачкообразно, тогда как их первые производные изменяются постепенно.
Фазовые переходы первого рода — фазовые переходы, при которых скачком изменяются первые производные термодинамических потенциалов по интенсивным параметрам системы (температуре или давлению).
Уравнение Клапейрона — Клаузиуса — термодинамическое уравнение, относящееся к квазистатическим (равновесным) процессам перехода вещества из одной фазы в другую
где L — удельная теплота фазового перехода, дельта u — изменение удельного объёма тела при фазовом переходе.
Тройная точка — точка на фазовой диаграмме, где сходятся три линии фазовых переходов. Тройная точка — это одна из характеристик вещества. Обычно тройная точка определяется значением температуры и давления, при котором вещество может равновесно находиться в трёх (отсюда и название) агрегатных состояниях: твёрдом, жидком и газообразном.
Фазовая диаграмма— графическое отображение равновесного состояния бесконечной физико-химической системы при условиях, отвечающих координатам рассматриваемой точки на диаграмме (давление, температура).
Статистическое толкование энтропии. Микро- и макросостояние системы. Термодинамическая вероятность. Формула Больцмана.
Статистическое толкование - энтропия является мерой неупорядоченности системы. Чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия.
Способ распределения частиц по ячейкам с учетом их номеров называется микросостоянием системы. Возможные микросостояния представлены в третьей колонке таблицы. Вероятность застать систему невзаимодействующих частиц в любом из перечисленных микросостояний одна и та же. Но число микросостояний, реализующих макросостояние 3, максимальное, и это макросостояние возникает чаще других. Оно является предпочтительным для системы.
Число микросостояний, соответствующих какому-либо макросостоянию системы, называется термодинамической вероятностью (статистическим весом) этого макросостояния. Термодинамическую вероятность будем обозначать буквой W. В последнем столбце приведены значения термодинамической вероятности для первых трех макросостояний. В простом рассматриваемом примере эти числа невелики, тогда как термодинамическая вероятность макросостояний систем, состоящих из большого числа частиц (порядка числа Авогадро), выражается, соответственно, числами очень высоких порядков.
Термодинамическая вероятность состояния системы — это число способов, которыми может быть реализовано данное состояние макроскопической системы, или 'число микросостояний, осуществляющих данное макросостояние.
Формула Больцмана позволяет дать статистическое толкование второго начала термодинамики:
Формула Больцмана:
S=k·lnW,
где k – постоянная, получившая позднее название постоянной Больцмана.