2.Розкрийте складні і складноскорочені силогізми.

Складним силогізмом, або полісилогізмом, називається умовивід, який складається з одного або двох силогізмів.

Полісилогізм — це ланцюг силогізмів. Будується він таким чином, що висновок попереднього силогізму (просилогізму) стає засновком наступного силогізму (епісилогізму) і т. д.

Полісилогізм має таку схему:

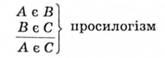
Існує два види полісилогізмів: прогресивні та регресивні.

Прогресивними називаються такі полісилотізми, у котрих висновок попереднього силогізму є більшим засновком наступного. Прикладом прогресивного полісилогізму є такий умовивід:

Регресивними називаються такі полісилогізми, у котрих висновок попереднього силогізму стає меншим засновком наступного. Наприклад:

У практиці мислення ми рідко маємо справу із повними полісилогізмами, користуючись звичайно скороченими формами. Полісилогізм, в котрому пропущені деякі засновки, називається соритом. "Сорит" — грецьке слово, в перекладі на українську мову означав "купа" засновків).

Є два види соритів: гокленіївський та аристотелівський.

Гокленїівський сорит здобувають із прогресивного полісилогізму, випускаючи в ньому проміжні висновки (більші засновки епісилогізмів).

Схема гокленіївського сориту:

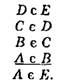
Приклад гокленіївського сориту:

Аристотелівський сорит — скорочена форма регресивного полісилогізму, в котрому випущені менші засновки. Схема цього сориту така:

До складноскорочених умовиводів відносяться також і епіхейрема. Епіхейремою називається такий складноскорочений силогізм, у котрому засновками є ентимеми. Приклад епіхейреми:

3.Дайте визначення розділовим умовиводам та розділово-категоричному і розділово-умовному силогізмам.

Ст.156,74.

4.Назвіть і розкрийте аксіоми силогізму.

Аксіома силогізму — це положення, яке обґрунтовує правомірність висновку із засновків категоричного силогізму. Вона має два такі формулювання:

1. Все, що стверджується (або заперечується) про клас предметів, може стверджувати (або заперечувати) про кожен предмет даного класу. Латинська формула нього правила така: dictum de omni et de nullo (буквально — сказане про все і ні про що), або коротше: dictum de omni.

2. Ознака ознаки речі є ознака самої речі; те, що суперечить ознаці речі, суперечить самій речі (nota note est nota rei).

Зміст цих речень полягає ось у чому. Якщо відомо, що клас предметів М має ознаку P, то з цього випливає, що будь-який окремий предмет S цього класу має ознаку Р. Наприклад, якщо відомо, що всі громадяни зобов'язані дотримуватися законів держави, то це означає, що й Петренко зобов'язаний дотримуватися законів держави.

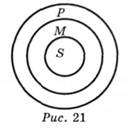
Відношення між термінами S—М—Р категоричного силогізму прийнято відтворювати за допомогою кіл як відношення між обсягами понять, що входять до засновку. Відношення обсягів понять буде таким: якщо обсяг поняття М входить до обсягу поняття Р, а обсяг поняття S входить до обсягу поняття М, то обсяг поняття 5 входить до обсягу поняття Р (рис. 21).

Відповідно, якщо відомо, що клас предметів М не містить ознак Р, то й усякий окремий предмет S, що входить до класу М, не має ознак Р. Так, якщо відомо, що жодна людина не може бути притягнена до кримінальної відповідальності інакше як за рішенням суду, то це означає, що й громадянин Петренко не може бути притягненим до карної відповідальності інакше як за ухвалою суду.

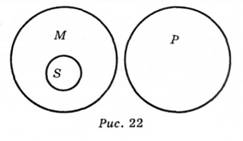
Відношення між термінами S—М—Р за обсягом тут таке: якщо обсяг поняття М повністю виключається із обсягу поняття Ру а обсяг поняття S входить до обсягу поняття М, то обсяг поняття S повністю виключається з обсягу поняття Р (рис. 22).

Аналогічно можна пояснити і другу формулу аксіоми: якщо річ А має ознаку В, а ознака ІЗ, у свою чергу, має ознаку С, то це означає, що А має також ознаку С.