- •Вопросы по курсу математическая логика и теория алгоритмов
- •Понятие высказывания.
- •Логические операции над высказываниями.
- •Формулы алгебры логики.
- •Равносильности.
- •1. Основные равносильности.
- •2. Равносильности, выражающие одни логические операции через другие.
- •3. Равносильности, выражающие основные законы алгебры логики.
- •Понятия тождественной истинности и ложности.
- •Функции алгебры логики. Свойства совершенства. Закон двойственности. Функции алгебры логики
- •Закон двойственности Закон двойственности
- •Дизъюнктивная нормальная форма (днф и сднф).
- •[Править]сднф
- •Конъюнктивная нормальная форма (кнф и скнф).
- •[Править]скнф
- •Проблема разрешимости.
- •Релейно-контактные схемы.
- •7.1 Релейно-контактные схемы
- •Элементы и множества. Задание множеств.
- •Операции над множествами.
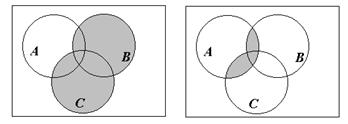
- •Диаграммы Эйлера-Венна.
- •Разбиения и покрытия множеств.
- •Свойства операций над множествами. Свойства операций над множествами
- •Упорядоченные пары. Декартово произведение множеств.
- •Отношения. Композиция, степень и ядро отношения.
- •[Править]Степень отношений
- •Функции. Инъективные, сюръективные и биективные функции.
- •Формулы исчисления высказываний.
- •Доказуемые формулы.
- •Аксиомы исчисления высказываний.
- •Правила вывода в исчислении высказываний.
- •Понятие выводимости формулы.
- •Правила выводимости.
- •Доказательство законов логики.
- •Связь между алгеброй высказываний и исчислением высказываний.
- •Основные понятия логики предикатов.
- •Исчисление предикатов. Основные понятия.
- •Логические операции над предикатами.
- •Кванторные операции.
- •Квантор всеобщности.
- •Квантор существования.
- •Отрицание предложений с кванторами.
- •Формулы логики предикатов.
- •Равносильные формулы логики предикатов.
- •Предваренная нормальная форма.
- •Общезначимость и выполнимость формул логики предикатов.
- •Применение логики предикатов для записи математических высказываний.
- •§9. Применение языка логики предикатов для записи математических предложений, определений, построения отрицания предложений.
- •9.1 Запись математических предложений и определений в виде формул логики предикатов.
- •9.2. Построение противоположный утверждений.
- •9.3 Прямая, обратная и противоположная теоремы.
- •9.4 Необходимые и достаточные условия.
- •9.5. Доказательство теорем методом от противного.
- •Алгоритмы. Основные свойства алгоритмов.
- •Частично рекурсивные и общерекурсивные функции. Тезис Черча.
- •Машина Тьюринга. Тезис Тьюринга.
Операции над множествами.
Операции над множествами. B}A или xB={x|x1) объединение: множество тех элементов х, которые принадлежат хотя бы одному множеству. A В}.A и хB={x|x2) пересечение: общие элементы A B}A и x3) разность множеств.A\B={x|x A}.В, то xB; xA, то x_B={x|x4) симметрическая разность A Иногда бывает удобно все рассматриваемые множества в некоторой теории считать подмножествами некоторого одного множества, которое в этом случае зовут универсальным U. AA- дополнение множества А. Это есть U/A=5) Булева алгебра множеств. Алгеброй зовут некоторое множество с введенными на нем операциями: A=- операции., где М- носитель, Школьная алгебра: A=. Возьмем U: A=- булева алгебра. 1) переместительный закон: AИB=BИA; AЗB=BЗA; 2) сочетательный закон: AИ(BИC)=(AИB)ИC; AЗ(BЗC)=(AЗB)ЗC 3) распределительный закон: AИ(BЗC)=(AИB)З(AИC); AЗ(BИC)=(AЗB)И(AЗC); 4) Not(not(A))=A – дополнение дополнения есть само дополнение 5) AИ0=A; AЗ0=0 6) AИU=U; AЗU=A; 7) AИA=A; AЗA=A 8) AИ`A=U; AЗ`A=0 9) закон поглощения AИ(AЗB)=A; AЗ(AИB)=A 10) закон де Моргана: not(AИB)= `AЗ`B; not(AЗB)= `AИ`B
Диаграммы Эйлера-Венна.
Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.
О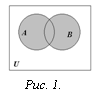 перации
над множествами рассматриваются для
получения новых множеств из уже
существующих.
перации
над множествами рассматриваются для
получения новых множеств из уже
существующих.
Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):
![]()
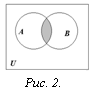
Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):
![]()
Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):
![]()
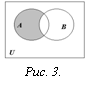
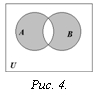
Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):
предыдущаяследующая
![]()
О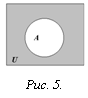 пределение. Абсолютным
дополнением множества
А называется множество всех тех элементов,
которые не принадлежат множеству А
(рис. 5):
пределение. Абсолютным
дополнением множества
А называется множество всех тех элементов,
которые не принадлежат множеству А
(рис. 5):
![]()
|
|
|
|
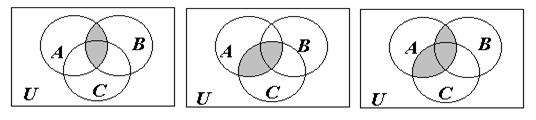
Пример
5. С
помощью диаграмм Эйлера – Венна
проиллюстрируем справедливость
соотношения ![]() (рис.
6).
(рис.
6).
|
|
|
|
![]()
![]()
Рис.6
Убедились, что в обоих случаях получаем равные множества. Следовательно, исходное соотношение справедливо.