11. Релейно-контактные схемы.

7.1 Релейно-контактные схемы

 

         Релейно-контактные схемы (их часто называют переключательными схемами) широко используются в технике автоматического управления.

 

            Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящее из следующих элементов:

 

1)      переключателей, которыми могут быть механические устройства, электромагнитные реле, полупроводники и т.д.;

2)      соединяющие их проводники;

3)      входы в схему и выходы из нее (клеммы, на которые подается электрическое напряжение). Они называются полюсами.

 

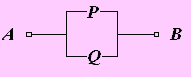
            Простейшая схема содержит один переключатель Р и имеет один вход А и один выход В.  Переключателю Р поставим в соответствии высказывание р, гласящее: - “Переключатель Р замкнут ”. Если р истинно, то импульс, поступающий на полюс А, может быть снят на полюсе В без потери напряжения, то есть схема пропускает ток. Если р ложно, то переключатель разомкнут и схема тока не проводит. Таким образом, если принять во внимание не смысл высказывания, а только его значение, то можно считать, что любому высказыванию может быть поставлена в соответсвие переключательная схема с двумя полюсами (двухполюсная схема).

 

            Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы.

 

 

            Так, конъюнкции двух высказываний   ставится в соответствие схема:

а дизъюнкции   - схема:

            Так как любая формула может быть записана в ДНФ или КНФ, то ясно, что каждой формуле алгебры логики можно поставить в соответствие некоторую РКС, а каждой РКС можно поставить в соответствие некоторую формулу алгебры логики.

            Пример 1. По данной формуле составить РКС  .

            Решение. Упростим данную формулу с помощью равносильных преобразований:

 

 

 

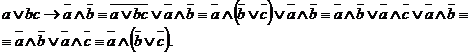
            Тогда РКС для данной формулы имеет вид:

 

            Пример 2. Упростить РКС:

 

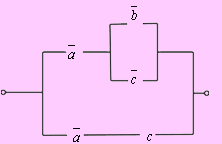
            Решение. Составим по данной РКС формулу (функцию проводимости) и упростим ее:

(к последним двум слагаемым применили закон поглощения).

            Тогда упрощенная схема выглядит так:

12. Элементы и множества. Задание множеств.

Множества. Основные понятия. Способы задания. Создатель теории множеств – Кантер(немец). Под множеством Кантер понимал скопления различных и определенных предметов, мыслимых как единое целое. Предметы, из которых состоят множества, зовут элементами множества. Слово определенный говорит о том, что если мы имеем множество и некоторый предмет, то всегда можно определить, принадлежит он множеству или нет. Слово различимый говорит о том, что если мы имеем два элемента множества, то всегда можно сказать, одинаковы они или нет. Но самое главное, что множество элементов, составляющих множество, мыслится как единое целое. Само множество может быть элементом другого множества. Что касается элементов множества, то они могут быть любой природы.  Множества могут быть конечными или бесконечными. И вообще мы можем не знать количество элементов в множестве. A. множество, не содержащее ни одного элемента, зовут пустым, и пишут 0. два множества А и В считаются равными, если они состоят из одних и тех же элементов. A={1,2,3}, B={1,1,1,2,2,3,3} – A=B. aAA, aЕсли элементами множества являются числа, то го зовут числовым. Множество изображается заглавными буквами, а его элементы – прописными. Некоторые определенные множества имеют определенные названия: N- множество натуральных чисел, Z- целых, Q- рациональных, I- иррациональных, R- действительных чисел, C- комплексных чисел. a  Множества можно задавать: 1) перечислением элементов A={1,a,b}, 2) с помощью определяющего свойства M={x|x-четные}.  А.В. Считается, что пустое множество является подмножеством любого множества. Два подмножества множества А – А и 0 – зовут несобственными подмножествами множества А. Все остальные – собственные. Если С – собственное подмножество множества А, то пишут СЕсли каждый элемент множества А является элементом множества В, то А зовут подмножеством В: А