2. Равносильности, выражающие одни логические операции через другие.

1.             

2.  .  

3.  .                                    

 4.  . 

5.  .  

6.  .

Здесь 3, 4, 5, 6 – законы Моргана.

Ясно, что равносильности 5 и 6 получаются из равносильностей 3 и 4, соответственно, если от обеих  частей последних взять отрицания и воспользоваться законом снятия двойного отрицания.

Таким образом, в доказательстве нуждаются первые четыре равносильности. Докажем одну из них : первую .

Так как при одинаковых логических значениях  x и y истинными являются формулы  , то истинной будет и конъюнкция  . Следовательно, в этом случае обе части равносильности имеют одинаковые истинные  значения.

            Пусть теперь  x и y имеют различные логические значения. Тогда будут ложными эквивалентность   и одна из двух импликаций   или  . Но при этом будет ложной и конъюнкция  .

            Таким образом, и в этом случае обе части равносильности имеют одинаковые логические значения.

             Аналогично доказываются равносильности  2 и 4.

Из равносительностей этой группы следует, что всякую формулу алгебры  логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.

Дальнейшее исключение логических операций невозможно. Так, если мы будем использовать только конъюнкцию, то уже такая формула как отрицание    не может быть выражена с помощью операции конъюнкции.

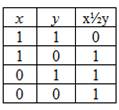
Однако существуют операции, с помощью которых может быть выражена любая из пяти  логических операций, которыми мы пользуемся. Такой операцией является, например, операция “Штрих Шеффера”. Эта операция обозначается символом     и определяется следующей таблицей истинности:

3. Равносильности, выражающие основные законы алгебры логики.

1.   - коммутативность конъюнкции.

2.   - коммутативность дизъюнкции.

3.   - ассоциативность конъюнкции.

4.   - ассоциативность дизъюнкции.

5.   - дистрибутивность конъюнкции относительно

                                                        дизъюнкции.

6.   - дистрибутивность дизъюнкции относительно

                                                        конъюнкции.

6. Понятия тождественной истинности и ложности.

ТОЖДЕСТВЕННАЯ ИСТИННОСТЬ, свойство сложных высказываний быть истинными в силу своей формально-логической структуры и смысла используемых в них логических операций. Будучи независимыми от содержания входящих в них конкретных высказываний, тождественно-истинные высказывания выступают в качестве логических законов.

Тождественно-истинной формулой называется формула, которая при любых комбинациях значений для входящих в нее переменных принимает значение истина. Тождественно-ложная формула – та, которая (соответственно) только значение ложь. Выполнимая формула может принимать значения как истина, так и ложь.

7. Функции алгебры логики. Свойства совершенства. Закон двойственности. Функции алгебры логики

Значение формулы алгебры логики полностью зависит от значений входящих в нее высказываний. Поэтому такая формула может считаться функцией входящих в нее элементарных высказываний. Например, (x  y)   z является функцией f(x, y, z). Естественно, значения этой функции и входящих в нее элементов могут принимать значения истина или ложь. Тождественно истинные или тождественно ложные функции представляют собой константы.

Каждую функцию алгебры логики можно записать в виде формулы или представить таблицей истинности. Как уже было отмечено выше, таблица истинности для n переменных содержит 2ⁿ строк. Следовательно, каждая функция алгебры логики принимает 2ⁿ значений, состоящих из 0 или 1. Общее же число наборов значений, состоящих из 0 и 1, длины 2ⁿ равно 2²ⁿ. В частности, число различных функций от одной переменной равно четырем.

х	f1(x)	f2(x)	f3(x)	F4(x)
0	1	1	0	0
1	1	0	1	0

Из этой таблицы следует, что две функции являются константами f₁(x) = 1 и – f₂(x) = x, а остальные f₃(x) =  x и f₄(x) = 0.

Свойства совершенства

Определение 4.11. Дизъюнктивную (конъюнктивную) нормальную форму от   переменных называют совершенной, если она обладает следующими свойствами:

1) каждая элементарная конъюнкция (дизъюнкция) содержит все   переменных,

2) все элементарные конъюнкции различны,

3) ни одна элементарная конъюнкция (дизъюнкция) не содержит одновременно переменную и ее отрицание,

4) ни одна элементарная конъюнкция (дизъюнкция) не содержит одну и ту же переменную дважды.

Свойства 1 – 4 ДНФ (КНФ) называют свойствами совершенства.

Определение 4.12. ДНФ (КНФ), обладающая свойствами совершенства, называют совершенной дизъюнктивной (конъюнктивной) нормальной формой.

Аббревиатура совершенных форм: СДНФ, СКНФ.

Справедливы утверждения.

Утверждение 1. Любая ненулевая булева функция   единственным образом представима в виде СДНФ от своих аргументов.

Утверждение 2. Любая ненулевая булева функция   единственным образом представима в виде СКНФ от своих аргументов.