25. Правила выводимости.

Правила выводимости.

Классическое исчисление высказываний использует два правила вывода:

Modus ponens. Из истинности условия импликации и истинности самой импликации следует истинность следствия импликации: α, α├ .

Правило одновременной подстановки. Из формулы α(р), где р – переменная, выводима формула α(R), где R – формула, получаемая заменой в α(р) каждого вхождения переменной р на формулу R: α (р) ├ α (R). В общем случае будем обозначать подстановку (x₁,…, x_n α₁,…, α_n).

Таким образом, доказуемой формулой называется всякая формула, которая или является аксиомой, или получается из доказуемых формул с помощью правил подстановки и Modus Ponens.

При практическом решении задач удобнее пользоваться не законами логики, а правилами из заменяющими. Внатуральном исчислении высказываний помимо правил Modus ponens и подстановки используют следующие:

Исключение конъюнкта. Из истинности конъюнкции следует истинность любого ее конъюнкта:

α₁  α₂  …  α_n ├ α_i.

Введение конъюнкции. Из списка истинных формул следует истинность их конъюнкции:

α₁, α₂, …, α_n ├ α₁  α₂  …  α_n.

Введение дизъюнкции. Из истинности формулы следует истинность ее дизъюнкции с любыми другими формулами:

α₁ ├ α₁  α₂  …  α_n.

Исключение двойного отрицания. Из истинности двойного отрицания формулы следует истинность ее самой:

α ├ α.

Простая резолюция (удаление дизъюнкта). Из истинности дизъюнкции и отрицания одного из ее дизъюнктов следует истинность формулы после удаления этого дизъюнкта:

α  ,  ├ α.

Резолюция. Из истинности двух дизъюнкций, одна из которых содержит дизъюнкт, а другая его отрицание следует формула, являющаяся дизъюнкцией исходных формул после удаления этого дизъюнкта:

α  ,   γ ├ α  γ.

26. Доказательство законов логики.

Правила выводимости, и особенно теорема дедукции, позволяют доказать ряд законов логики.

1. Закон перестановки посылок.

├(x→(y→z)) →(y→(x→z)). (1)

Доказательство:

Можно показать, что (аналогично тому, как это делалось в примере §4) из совокупности формул Н={x→(y→ z ), y, x} следует вывод x→(y→ z), y, x, y→ z, z, т. е. из совокупности Н выводима формула z. Тогда по обобщенной теореме дедукции доказуема формула (1). И тогда по ПЗ из закона перестановки посылок вытекает правило перестановки посылок в доказуемых формулах: ├(x→(y→ z))

├(y→(x→ z)). (2)

Действительно, если ├x→(y→ z), (2), то из (1) и (2) по правилу заключения следует ├y→(x→z).

2. Закон соединения посылок.(формула (25) законов логики высказываний).

├(x→(y→ z)) →( →z). (3)

Доказательство:

Можно показать, что из совокупности формул Н={x→(y→ z ), } следует вывод x→(y→ z), , → х, → y, x, y, y→ z, z, т. е. из совокупности Н выводима формула z. Тогда по обобщенной теореме дедукции доказуема формула (3).

Из закона соединения посылок вытекает правило соединения посылок в доказуемых формулах: ├(x→(y→z))

├ →z. (4)

Действительно, если ├x→(y→z), (4), то из (3) и (4) по правилу заключения следует ├ →z.

3. Закон разъединения посылок (формула (25)) .

├( →z) →(x→(y→z)). (5)

Так как из совокупности формул Н={x, y, →z} следует вывод x, y, →z, , z, то из совокупности формул Н выводима формула z. Тогда по обобщенной теореме дедукции доказуема формула (5).

Из закона разъединения посылок вытекает правило разъединения посылок в доказуемых формулах: ├ → z

├х→(y→z). (6)

Действительно, если ├ →z)), (6), то из (5) и (6) по правилу заключения следует

├х→(y→z).

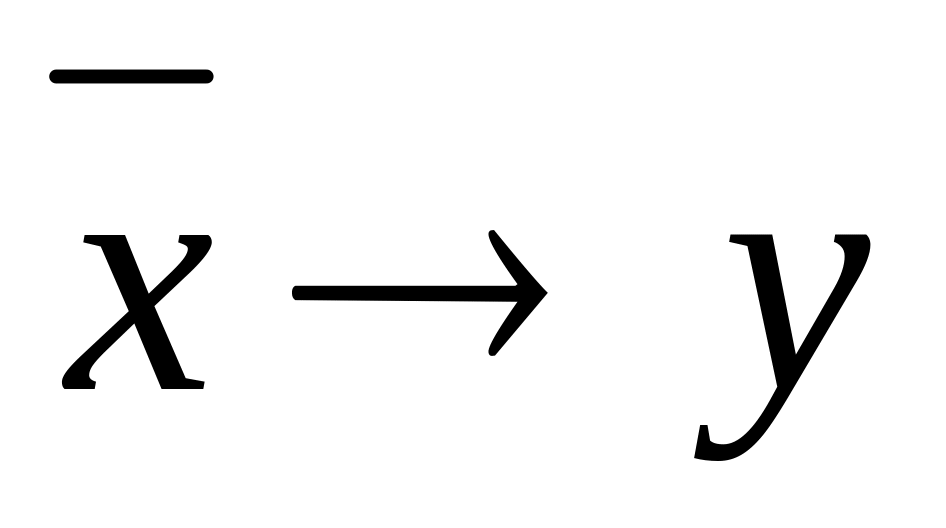4. ├х→( ). (7)

Доказательство:

Сделаем подстановки в аксиомы и : и .

В результате получим доказуемые формулы:

├х→( ), (8) и ├ . (9)

Из формул (8)и (9)по правилу силлогизма следует : ├ .

Используя закон соединения посылок, получим: ├ .

Используя правило снятия двойного отрицания, получим : ├ .

И, наконец, применяя закон разъединения посылок, получим (7).

5. Закон исключенного третьего: ├ .

Доказательство:

Воспользуемся доказуемой формулой ├ . (10)

и, сделав в ней подстановку , получим :

├ . (11)

Также сделаем подстановку в формуле (7), заменяя на , а y на :

├ ( ). (12)

Используя закон соединения посылок, будем иметь : ├ . (13)

Из формул (11) и (13) по правилу силлогизма получаем ├ . (14)

Из формулы (14) по правилу контрапозиции следует├ .

Используя оба правила снятия двойного отрицания, получаем ├ (15)

Пусть теперь y- любая доказуемая формула R, тогда из формул ├R, ├R по правилу заключения получаем ├ .

6.├ . Примем этот закон без доказательства.