Вопрос 5

Анализ размерностей

метод установления связи между физическими величинами, существенными для изучаемого явления, основанный на рассмотрении размерностей этих величин.

В основе анализа размерностей лежит требование, согласно которому в уравнении, выражающем связь между физическими величинами, размерности левой и правой части уравнения должны быть одинаковы.

Подобие явлений и его признаки

Подобие явлений означает, что данные о протекании процессов, полученные при изучении одного явления, можно распространить на все явления, подобные данному. Явление представляет собой совокупность процессов, описываемых уравнениями, связывающими параметры процессов и параметры системы, записанными в выбранной системе координат. Явления будут абсолютно подобны друг другу, если существует полное соответствие всех геометрических размеров рассматриваемых систем и всех изменяющихся во времени и пространстве величин, т.е. процессов, протекающих в этих системах. ^ Аффинное подобие – Не выполняется геометрическое соответствие. Абсолютное подобие явлений - требуется, чтобы во все сходственные моменты времени во всех сходственных точках пространства параметры процессов и элементов одной системы были пропорциональными соответствующим параметрам другой системы. ^ Полное подобие – подобие тех процессов, которые в основном определяют исследуемое явление. Неполное подобие – подобие протекания процессов только во времени или только в пространстве. ^ Приближенное подобие - связано с некоторыми упрощающими допущениями, заранее оцениваемыми качественно. Физическое подобие - осуществляется при одинаковой физической природе подобных явлений. ^ Математическое подобие - требует только соответствия между параметрами сравниваемых процессов, в частном случае – одинаковой форме уравнений, описывающих физические разнородные явления.

Вопрос 6 Первая теорема подобия

Кратко эту теорему можно сформулировать следующим образом: у подобных процессов некоторые соотношения параметров, называемые критериями подобия, численно одинаковы.  - первый процесс,  – второй процесс. , ->  . -> , ->  , ->   ,   -> P₁ = n₁R₁, P₂ = n₂R₂, …, P_n = n_nR_n . -> ₁ = N₁₁ , ₂ = N₂₂,…, _n = N_n_n, ->  . -> ,  , …,  , -> 

Вопрос 8

Монте Карло – это множество статистических

методов, используемых для решения

физических и математических задач.

В этих методах для моделирования

используются последовательности случайных

чисел.

z Методы Монте Карло наиболее удобны для

моделирования случайных и вероятностных

процессов.

Первоначально метод Монте-Карло использовался главным образом для решения задач нейтронной физики, где традиционные численные методы оказались мало пригодными. Далее его влияние распространилось на широкий класс задач статистической физики, очень разных по своему содержанию. К разделам науки, где все в большей мере используется метод Монте-Карло, следует отнести задачи теории массового обслуживания, задачи теории игр и математической экономики, задачи теории передачи сообщений при наличии помех и ряд других.

Метод Монте-Карло можно определить как метод моделирования случайной величины с целью вычисления характеристик их распределений. Как правило, составляется программа для осуществления одного случайного испытания. Затем это испытание повторяется N раз, причем каждый опыт не зависит от остальных, и результаты всех опытов усредняются. Это значит, что число испытаний должно быть достаточно велико, поэтому метод существенно опирается на возможности компьютера.

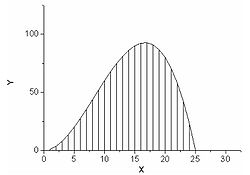
Рисунок 2. Численное интегрирование функции детерминистическим методом

Предположим, необходимо взять интеграл от некоторой функции. Воспользуемся неформальным геометрическим описанием интеграла и будем понимать его как площадь под графиком этой функции.

Для определения этой площади можно воспользоваться одним из обычных численных методов интегрирования: разбить отрезок на подотрезки, подсчитать площадь под графиком функции на каждом из них и сложить. Предположим, что для функции, представленной на рисунке 2, достаточно разбиения на 25 отрезков и, следовательно, вычисления 25 значений функции. Представим теперь, мы имеем дело с  -мерной функцией. Тогда нам необходимо   отрезков и столько же вычислений значения функции. При размерности функции больше 10 задача становится огромной. Поскольку пространства большой размерности встречаются, в частности, в задачах теории струн, а также многих других физических задачах, где имеются системы со многими степенями свободы, необходимо иметь метод решения, вычислительная сложность которого бы не столь сильно зависела от размерности. Именно таким свойством обладает метод Монте-Карло.

Обычный алгоритм Монте-Карло интегрирования[править | править исходный текст]

Предположим, требуется вычислить определённый интеграл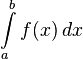 

Рассмотрим случайную величину  , равномерно распределённую на отрезке интегрирования  . Тогда   также будет случайной величиной, причём её математическое ожидание выражается как 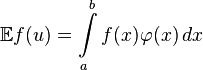, где   — плотность распределения случайной величины  , равная   на участке  .

Таким образом, искомый интеграл выражается как .

Но матожидание случайной величины   можно легко оценить, смоделировав эту случайную величину и посчитав выборочное среднее.

Итак, бросаем   точек, равномерно распределённых на  , для каждой точки   вычисляем  . Затем вычисляем выборочное среднее:  .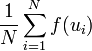

В итоге получаем оценку интеграла: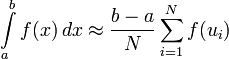 

Точность оценки зависит только от количества точек  .

Этот метод имеет и геометрическую интерпретацию. Он очень похож на описанный выше детерминистический метод, с той разницей, что вместо равномерного разделения области интегрирования на маленькие интервалы и суммирования площадей получившихся «столбиков» мы забрасываем область интегрирования случайными точками, на каждой из которых строим такой же «столбик», определяя его ширину как  , и суммируем их площади.

Геометрический алгоритм Монте-Карло интегрирования[править | править исходный текст]

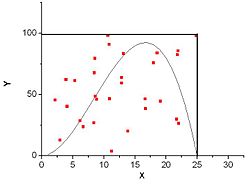
Рисунок 3. Численное интегрирование функции методом Монте-Карло

Для определения площади под графиком функции можно использовать следующий стохастический алгоритм:

• ограничим функцию прямоугольником (n-мерным параллелепипедом в случае многих измерений), площадь которого 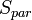  можно легко вычислить; любая сторона прямоугольника содержит хотя бы 1 точку графика функции, но не пересекает его;

• «набросаем» в этот прямоугольник (параллелепипед) некоторое количество точек (  штук), координаты которых будем выбирать случайным образом;

• определим число точек ( 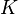 штук), которые попадут под график функции;

• площадь области, ограниченной функцией и осями координат, 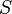  даётся выражением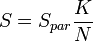 

Для малого числа измерений интегрируемой функции производительность Монте-Карло интегрирования гораздо ниже, чем производительность детерминированных методов. Тем не менее, в некоторых случаях, когда функция задана неявно, а необходимо определить область, заданную в виде сложных неравенств, стохастический метод может оказаться более предпочтительным.

Вопрос 9

Случайной величиной называется отображение множества элементарных событий в множество вещественных

Обычно наблюдаются и изучаются не элементарные события, множество которых нам совершенно неизвестно, а именно случайные величины. Чтобы задать их вероятностное поведение, нужно задать вероятности того, что случайная величина принимает то или иное значение. Рассмотренный нами пример случайной величины мы сможем опеределить так:       

x	2	3	4	5	6	7	8	9	10	11	12
P(x)	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36