Билет №34

1. Механические колебания. Виды колебаний. Периодические и гармонические колебания. Свободные, незатухающие и затухающие колебания.

2. Структурная схема съема, передачи и регистрации медико-биологической информации. Датчики медико-биологической информации.

 Колебания. Периодические колебания.

Гармонические колебания

Колебаниями называют процессы, отличающиеся той или иной степенью повторяемости.

Повторяющиеся процессы непрерывно происходят внутри любого живого организма, например: сокращения сердца, работа легких; мы дрожим, когда нам холодно; мы слышим и разговариваем благодаря колебаниям барабанных перепонок и голосовых связок; при ходьбе наши ноги совершают колебательные движения. Колеблются атомы, из которых мы состоим. Мир, в котором мы живем, удивительно склонен к колебаниям.

В зависимости от физической природы повторяющегося процесса различают колебания: механические, электрические и т.п. В настоящей лекции рассматриваются механические колебания.

Периодические колебания

Периодическими называют такие колебания, при которых все характеристики движения повторяются через определенный промежуток времени.

Для периодических колебаний используют следующие характеристики:

•  период колебаний Т, равный времени, в течение которого совершается одно полное колебание;

•  частота колебаний ν, равная числу колебаний, совершаемых за одну секунду (ν = 1/Т);

•  амплитуда колебаний А, равная максимальному смещению от положения равновесия.

Гармонические колебания

Особое место среди периодических колебаний занимают гармонические колебания. Их значимость обусловлена следующими причинами. Во-первых, колебания в природе и в технике часто имеют характер, очень близкий к гармоническому, и, во-вторых, периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний.

Гармонические колебания - это колебания, при которых наблюдаемая величина изменяется во времени по закону синуса или косинуса:

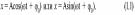В математике функции этого вида называют гармоническими, поэтому колебания, описываемые такими функциями, тоже называют гармоническими.

Положение тела, совершающего колебательное движение, характеризуется смещением относительно равновесного положения. В этом случае величины, входящие в формулу (1.1), имеют следующий смысл:

х - смещение тела в момент времени t;

А - амплитуда колебаний, равная максимальному смещению;

ω - круговая частота колебаний (число колебаний, совершаемых за 2π секунд), связанная с частотой колебаний соотношением

φ = (ωt +φ₀) - фаза колебаний (в момент времени t); φ₀ - начальная фаза колебаний (при t = 0).

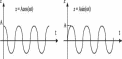Рис. 1.1. Графики зависимости смещения от времени для х(0) = А и х(0) = 0

1.2. Свободные колебания. Незатухающие и затухающие колебания

Свободными или собственными называются такие колебания, которые происходят в системе, предоставленной самой себе, после того как она была выведена из положения равновесия.

Примером могут служить колебания шарика, подвешенного на нити. Для того чтобы вызвать колебания, нужно либо толкнуть шарик, либо, отведя в сторону, отпустить его. При толчке шарику сообщается кинетическаяэнергия, а при отклонении - потенциальная.

Свободные колебания совершаются за счет первоначального запаса энергии.

Свободные незатухающие колебания

Свободные колебания могут быть незатухающими только при отсутствии силы трения. В противном случае первоначальный запас энергии будет расходоваться на ее преодоление, и размах колебаний будет уменьшаться.

В качестве примера рассмотрим колебания тела, подвешенного на невесомой пружине, возникающие после того, как тело отклонили вниз, а затем отпустили (рис. 1.2).

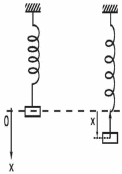Рис. 1.2. Колебания тела на пружине

Со стороны растянутой пружины на тело действует упругая сила F, пропорциональная величине смещения х:

Постоянный множитель k называется жесткостью пружины и зависит от ее размеров и материала. Знак «-» указывает, что сила упругости всегда направлена в сторону, противоположную направлению смещения, т.е. к положению равновесия.

При отсутствии трения упругая сила (1.4) - это единственная сила, действующая на тело. Согласно второму закону Ньютона (ma = F):

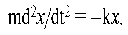После переноса всех слагаемых в левую часть и деления на массу тела (m) получим дифференциальное уравнение свободных колебаний при отсутствии трения:

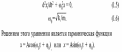Величина ω₀ (1.6) оказалась равной циклической частоте. Эту частоту называют собственной.

Таким образом, свободные колебания при отсутствии трения являются гармоническими, если при отклонении от положения равновесия возникает упругая сила (1.4).

Собственная круговая частота является основной характеристикой свободных гармонических колебаний. Эта величина зависит только от свойств колебательной системы (в рассматриваемом случае - от массы тела и жесткости пружины). В дальнейшем символ ω₀ всегда будет использоваться для обозначения собственной круговой частоты (т.е. частоты, с которой происходили бы колебания при отсутствии силы трения).

Амплитуда свободных колебаний определяется свойствами колебательной системы (m, k) и энергией, сообщенной ей в начальный момент времени.

При отсутствии трения свободные колебания, близкие к гармоническим, возникают также и в других системах: математический и физический маятники (теория этих вопросов не рассматривается) (рис. 1.3).

Математический маятник - небольшое тело (материальная точка), подвешенное на невесомой нити (рис. 1.3 а). Если нить отклонить от положения равновесия на небольшой (до 5°) угол α и отпустить, то тело будет совершать колебания с периодом, определяемым по формуле

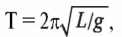где L - длина нити, g - ускорение свободного падения.

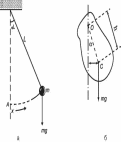Рис. 1.3. Математический маятник (а), физический маятник (б)

Физический маятник - твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси. На рисунке 1.3 б схематически изображен физический маятник в виде тела произвольной формы, отклоненного от положения равновесия на угол α. Период колебаний физического маятника описывается формулой

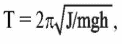где J - момент инерции тела относительно оси, m - масса, h - расстояние между центром тяжести (точка С) и осью подвеса (точка О).

Момент инерции - это величина, зависящая от массы тела, его размеров и положения относительно оси вращения. Вычисляется момент инерции по специальным формулам.

Свободные затухающие колебания

Силы трения, действующие в реальных системах, существенно изменяют характер движения: энергия колебательной системы постоянно убывает, и колебания либо затухают, либо вообще не возникают.

Сила сопротивления направлена в сторону, противоположную движению тела, и при не очень больших скоростях пропорциональна величине скорости:

График таких колебаний представлен на рис. 1.4.

В качестве характеристики степени затухания используют безразмерную величину, называемуюлогарифмическим декрементом затухания λ.

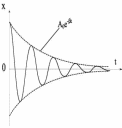Рис. 1.4. Зависимость смещения от времени при затухающих колебаниях

Логарифмический декремент затухания равен натуральному логарифму отношения амплитуды предыдущего колебания к амплитуде последующего колебания.

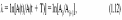где i - порядковый номер колебания.

Нетрудно видеть, что логарифмический декремент затухания находится по формуле

Сильное затухание. При

выполнении условия β ≥ ω₀ система возвращается в положение равновесия, не совершая колебаний. Такое движение называется апериодическим. На рисунке 1.5 показаны два возможных способа возвращения в положение равновесия при апериодическом движении.

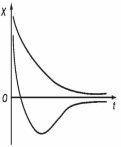Рис. 1.5. Апериодическое движение