6.6. Обобщенная система управляемый преобразователь-двигатель

В курсе «Теория электропривода» изучаются наиболее общие закономерности, свойственные разомкнутым и замкнутым системам электропривода, поэтому в предшествующем изложении при изучении особенностей отдельных видов электромеханических преобразователей значительное внимание было уделено установлению общности процессов электромеханического преобразования энергии в различных двигателях и в §4.3 введено понятие обобщенной разомкнутой электромеханической системы с линейной механической характеристикой. Это позволило выполнить в гл. 4 анализ динамики разомкнутых систем в обобщенном виде, проиллюстрировав частные проявления общих свойств в конкретных электроприводах примерами расчета.

Проведенный в данной главе анализ особенностей основных разновидностей регулируемого электропривода - систем Г-Д, ТП-Д и ПЧ-АД - также дает основания для обобщений. Сравнивая структурные схемы этих систем, которые ранее были приведены на рис.6.5,б, 6.11,б и 6.14, можно установить их принципиальную аналогию в пределах принятых допущений. Опираясь на эту аналогию, можно с учетом упругих механических связей в системе электропривода записать следующую систему дифференциальных уравнений для обобщенной системы управляемый преобразователь - двигатель (УП-Д):

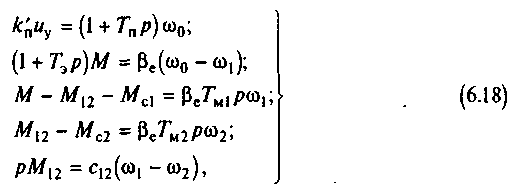
где

Для системы Г-Д

Для системы ТП-Д

Для системы ПЧ-АД

Структурная схема обобщенной системы УП-Д, соответствующая (6.18), представлена на рис.6.15,а. В пределах принятых допущений эта структура в дальнейшем используется для анализа наиболее общих закономерностей, характерных для регулиро вания основных координат электропривода. Из приведенных пояснений к формуле (6.18) вытекает, что специфика конкретных :систем при рассмотрении свойств системы УП-Д отражается в значениях обобщенных параметров и их связи с конкретными параметрами машин.

С труктурная схема системы УП-Д, приведенная на рис.6.15,а, может использоваться при анализе влияния обратных связей на динамику упругих электромеханических систем. Для анализа общих возможностей и свойств электропривода при регулировании тока, момента, скорости и положения в дальнейшем используется обобщенная структура электропривода по системе УП-Д при жестких механических связях (с₁₂=), представленная на рис.6.15,б.

6.7. Связь показателей регулирования с лачх разомкнутого контура регулирования

Математические методы теории автоматического управления являются основой для синтеза замкнутых систем регулируемого электропривода с заданными статическими и динамическими показателями. Наиболее общие и широко используемые на практике представления о возможностях реализации заданных показателей регулирования дает известная из курса теории управления связь основных показателей с ЛАЧХ разомкнутого контура регулирования.

С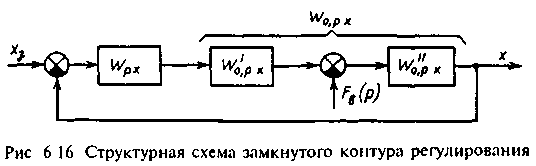 труктурная схема контура регулирования, преобразованная к единичной обратной связи для удобства определения ошибки регулирования, представлена на рис.6.16. Передаточная функция разомкнутого контура по управляющему воздействию [при Fн(p)=0] имеет вид

где W_px и W_opx - передаточные функции соответственно регулятора величины х и объекта регулирования; W''_opx - передаточная функция объекта регулирования по возмущающему воздействию F_B.

Если для рассматриваемого контура регулирования определить передаточные функции ошибки по управлению х_з и по возмущению F_B то с их помощью можно получить известное из теории управления изображение суммарной ошибки замкнутого контура регулирования:

Пусть в общем случае передаточная функция разомкнутого контура регулирования имеет вид

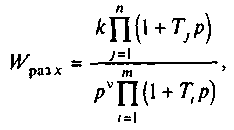
где v - порядок астатизма контура; m, п - число последовательно включенных соответственно инерционных и форсирующих звеньев; k - коэффициент усиления разомкнутого контура.

Для того чтобы после замыкания контура отрицательной обратной связью по регулируемой координате обеспечивались требуемая точность и динамические показатели качества регулирования, ЛАЧХ разомкнутого контура должна иметь вполне определенный вид и параметры. Общая форма желаемой ЛАЧХ разомкнутого контура представлена на рис.6.17.

Ч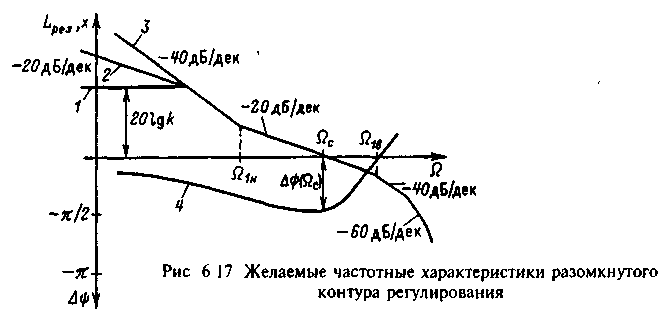 тобы удовлетворить требованиям, предъявляемым к электроприводу в отношении точности регулирования координаты, необходимо сформировать низкочастотную область характеристики определенного вида. Эта область определяется коэффициентом k и порядком астатизма системы v. Если v=0, т. е. в разомкнутом контуре регулирования отсутствуют интегрирующие звенья, система является статической системой регулирования, при этом статическая ошибка регулирования определяется в соответствии с (6.19) коэффициентом усиления контура k . Для получения требуемой точности необходимо предусмотреть коэффициент усиления, отвечающий условию

где х_{3 max} - заданное значение переменной; х_доп - допустимая ошибка регулирования.

Если требуется исключить статическую ошибку по заданию, необходимо, чтобы в контуре был интегрирующий элемент (v=1), при этом будет иметься динамическая ошибка, возникающая при изменениях задания Увеличение порядка астатизма (v=2) повышает при надлежащем коэффициенте усиления k динамическую точность регулирования.

Низкочастотная часть желаемой ЛАЧХ, соответствующая v=0, 1,2, представлена на рис.6.17 в виде отрезков прямых 1-3 Нетрудно видеть, что повышение порядка астатизма увеличивает значения комплексного коэффициента усиления в низкочастотной части и динамическая точность регулирования возрастает тем в большей степени, чем в более широком диапазоне частот обеспечивается повышение амплитуд.

Динамические показатели качества регулирования определяются главным образом среднечастотной асимптотой ЛАЧХ L_{раз х}.

Для получения достаточного запаса устойчивости необходимо, чтобы в районе частоты среза c. был достаточно протяженный участок с наклоном -20 дБ/дек. Чем шире этот участок, тем выше на частоте среза запас по фазе (_С)=--(_C), где () - ФЧХ контура. Зависимость (W) показана на рис.6.17 (кривая 4).

От запаса по фазе на частоте среза зависят колебательность и перерегулирование (см. рис.6.3):

Частота среза определяет быстродействие контура регулирования. С ней связано время регулирования

а также время максимума перерегулирования

Ближайшая нижняя частота сопряжения _1H влияет на перерегулирование: по мере приближения _1н к частоте среза запас по фазе (_С) уменьшается и перерегулирование возрастает. Ближайшая к частоте среза верхняя частота сопряжения _1B и вся высокочастотная часть ЛАЧХ L_pa3x сказывается на начальном участке переходного процесса.

Чем ближе частоты сопряжения этой области к частоте среза и чем выше наклон удаленной асимптоты, тем больше показанный на рис.6.3 участок запаздывания движения t₃.

Таким образом, требования к точности и динамическим показателям электропривода при регулировании определенной переменной позволяют конкретизировать количественные характеристики желаемой ЛАЧХ разомкнутого контура. При известной ЛАЧХ объекта регулирования переменной х L_opx желаемая ЛАЧХ разомкнутого контура L_разх позволяет определить требуемую ЛАЧХ регулятора, вводимого в контур регулирования:

Далее решается техническая задача подбора удобной схемы регулятора и определения его параметров, исходя из (6.23). Этот путь синтеза универсален и позволяет наиболее полно учесть весь комплекс предъявляемых к электроприводу требований в отношении как точности регулирования, так и его динамических показателей в наиболее сложных случаях.

Однако при проектировании электроприводов массового применения, при создании унифицированных систем электропривода широкого назначения этот путь сложен и не обеспечивает достаточной конкретности получаемых динамических свойств регулируемого электропривода.

Для случаев, когда в основу синтеза могут быть положены динамические показатели, в теории электропривода разработан инженерный метод последовательной коррекции с использованием подчиненных контуров регулирования.

Этот метод позволяет получить вполне определенные динамические свойства регулируемого электропривода, соответствующие конкретным так называемым стандартным настройкам контуров регулирования.