Можливі ризико-прибуткові характеристики портфелю з двох цінних паперів g,d , в залежності від портфельної ваги першого активу

№ п/п	Вага першого активу у портфелі, в %	Сподіваний відносний квартальний прибуток портфелю, в долях	Ризик портфелю (середньо- квадратичне відхилення)
0	1	2	3

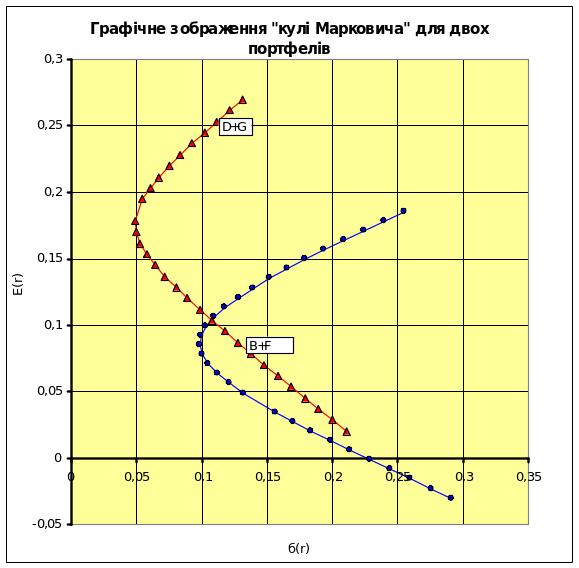
Рис. 17. Графічне зображення «кулі Марковича» для двох портфелів

Результати обчислень сподіваних прибутків та ризику портфелю за формулами (17-18) заносяться в відповідні колонки таблиці (колонки 2, 3).

Аналогічний розрахунок проектант проводить і для іншого портфелю з двох цінних паперів.

На основі проведених розрахунків проектантом робляться висновки про сумісність даних цінних паперів у портфелі.

За погодженням з керівником з протабульованих параметрів портфелів проектантом обирається по одному портфелю з мінімальним значенням ризику (точка MVP на графіку «кулі Марковіча»). Для даних портфелів за раніше наведеними формулами (17,18) уточнюється значення прибутку та ризику.

Оскільки обрані нами портфелі з точки зору ризико-прибуткових характеристик нічим не відрізняються від звичайних цінних паперів, то наступною стадією є проектування портфелю котрий складатиметься з двох портфелів, тобто буде містити в собі чотири початкових фондових активи.

Розрахунок такого портфелю здійснюється за аналогією до розрахунку портфелів з двох звичайних активів. В процесі формування даного портфелю так як і двох попередніх необхідно розрахувати параметри відносних очікуваних прибутків та величини ризику при різних пропорціях активів, що входять в даний портфель. В ході формування даного портфелю для розрахунку відносних сподіваних квартальних прибутків та ризику проектантом використовуються відповідні формули (17, 18). Результати обчислень за даними формулами так само заносяться в відповідну таблицю, приклад котрої наведено вище (див. табл. 6). На основі розрахованих даних будується третя «куля Марковіча» (рис. 18).

Після проведення розрахунків двох портфелів, що складаються з двох активів кожен та одного чотирьох активного портфелю проектантом формується ще один портфель, котрий на цей раз складається з трьох активів.

Для початку вибирається вихідний матеріал для формування такого портфелю. За обов’язковим погодженням з керівником проекту перш за все вибираються три види цінних паперів серед раніше вибраних чотирьох видів. Стараються при цьому обрати цінні папери з найкращими ризико-прибутковими характеристиками, проте кожен конкретний випадок обговорюється окремо. Критерієм придатності даних цінних паперів для формування портфелю можуть виступати коваріаційні співвідношення між ними. Даних три види цінних паперів і є вихідним матеріалом для побудови портфелю з трьох активів.

Рис. 18. Графічне зображення «кулі Марковича» для двох портфелів та портфелю з двох активів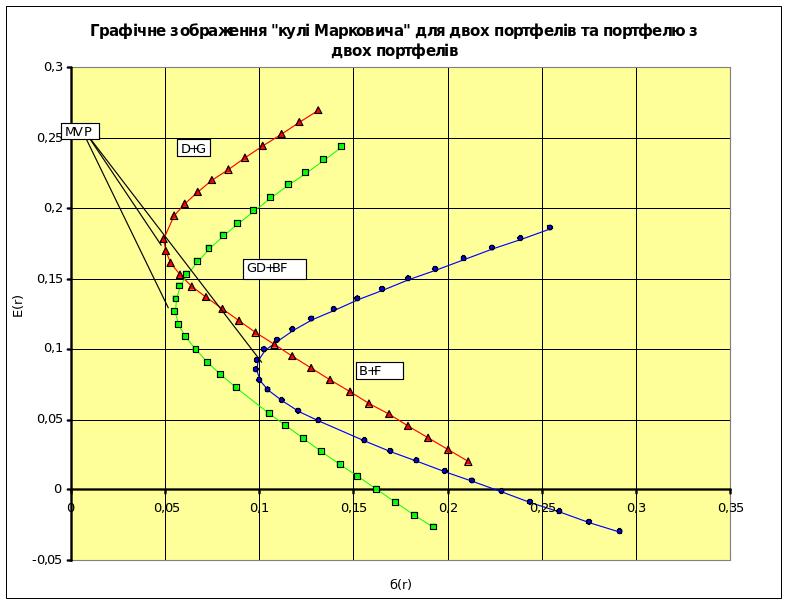

При побудові та графічному зображенні характеристик портфелю з трьох активі використовують координатну площину для котрої вздовж горизонтальної осі відкладають частку одного активу (портфельну вагу) в загальній структурі портфелю, а вздовж другої осі відкладають портфельну вагу другого активу. Портфельну вагу третього активу зображати немає потреби, оскільки її можна визначити виходячи з того, що сума портфельних ваг активів одного портфелю повинна дорівнювати одиниці.

Тобто для портфелю, що складається з трьох активів A, B, C справедливе співвідношення:

(19)

де - портфельні ваги активів A, B та C у портфелі.

Звідси:

(20)

Формула демонструє можливість отримання від»ємної величини портфельної ваги, що має економічне обґрунтування у вигляді концепції короткого продажу. Проте на практиці часто використання даної концепції суперечить принципам фінансової політики інституційних інвесторів, а отже на графічній моделі (рис. 19) зображена обмежена область місцезнаходження портфелів при формуванні котрих немає необхідності використовувати дану концепцію. Ця область зображена у вигляді одиничного трикутника.

В ході виконання проекту виконавець наносить на графічну модель трьох активного портфелю ізолінії сподіваних відносних прибутків котрі являють собою геометричне положення на моделі портфелів з однаковою величиною сподіваних відносних прибутків (рис. 20).

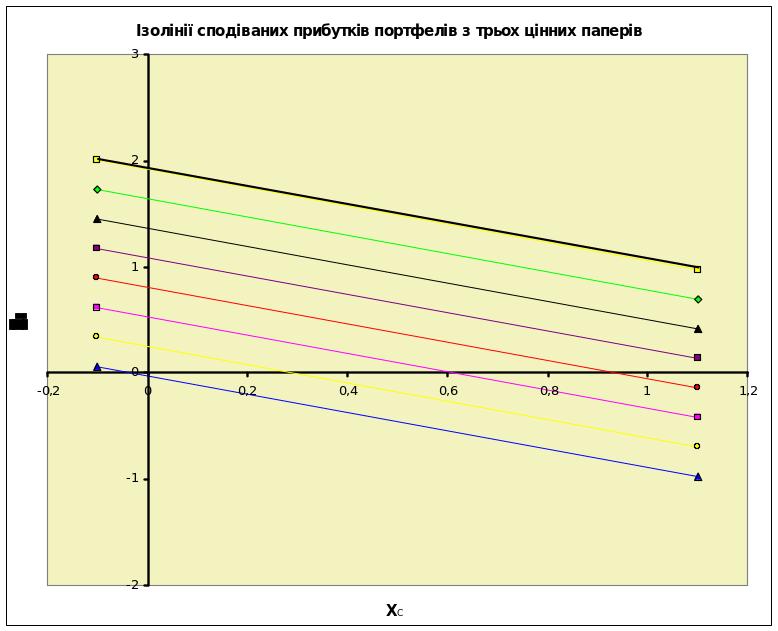
Рис. 20. Ізолінії сподіваних прибутків портфелів з трьох цінних паперів

В загальному випадку рівняння ізолінії сподіваних відносних прибутків виражається лінійним співвідношенням між першими двома портфельними вагами портфелю з трьох активів, тобто:

(21)

де - відповідно вільний член та коефіцієнт нахилу ізолінії сподіваних прибутків портфелю.

Для портфелю, що складається з трьох активів A,B,C кут нахилу всіх ізоліній сподіваних прибутків є однаковим і не залежить від сподіваної величини відносного доходу портфелю. Його можна визначити за формулою:

(22)

Проектант розраховує дану величину для свого проекту, при цьому використовує обчислені раніше (табл. 1, колонка 7) значення сподіваних прибутків.

Вільний член ізолінії сподіваних прибутків залежить від сподіваного відносного прибутку портфелів котрі зображаються у вигляді конкретної ізолінії сподіваних прибутків. Отже для його обчислення слід перш за все задатись величиною сподіваних прибутків портфелів, для яких будуватиметься дана лінія. Розрахунок вільного члена ізолінії сподіваних прибутків портфелю можна здійснювати за формулою:

(23)

При виконанні курсового проекту виконавець будує стільки ізоліній сподіваних прибутків портфелів, скільки їх є необхідно для того, щоб повністю перекрити одиничний трикутник на графіку, так як це показано вище на графічній моделі (рис. 19). Таким чином проектант самостійно вибирає початкове значення сподіваних прибутків портфелю для першої ізолінії. Всі наступні ізолінії розраховуються проектантом для портфелів, що за своїми прибутками віддалені від початкової лінії на 2.0 %. Тобто, проектант може, наприклад, розраховувати параметри ізоліній для портфелів за якими сподіваються отримати 12%, 14%, 16%, 18%, 20%, як це показано на моделі (рис. 20.).

Результати обчислених параметрів ізоліній приводяться проектантом в табличному виді (див. табл. 7.).

Таблиця 7