Литература
1. Рутесвард О. Невозможные фигуры. - М.: Стройиздат, 1990.
2. Сайт В. Алексеева www.impworld.narod.ru.
3. Сайт Д. Ракова www.rakov.de.
4. Сайт «Наука и жизнь» http:// nauka.relis.ru
Приложение 1.
Картины с использованием невозможных фигур
Вильям Хогард. "Невозможная перспектива", где намеренно сделано по меньшей мере четырнадцать ошибок в перспективе.
Мадонна с младенцем. 1025 год.
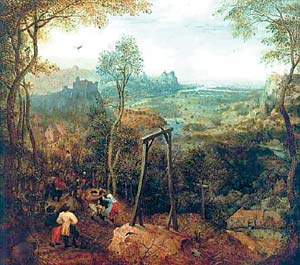
Питер Брейгель. "Сорока на виселице". 1568 год.
Марсель Дюшамп. Рекламная картинка с кроватью невозможной конструкции.
Мауриц Корнелиус Эшер. "Восхождение и спуск".
Роджер Пенроуз. "Невозможный треугольник". 1954 год.
Построение "невозможного треугольника".
Скульптура "Невозможный треугольник", вид с разных сторон. Она построена из криволинейных элементов и выглядит невозможной только из одной точки.
"Mail to" (Р1-4). тушь, карандаш. На рисунке - хорошо известный символ электронной почты @. Он сложен из реальных кирпичиков, но пересечение образованных ими линий невозможно.
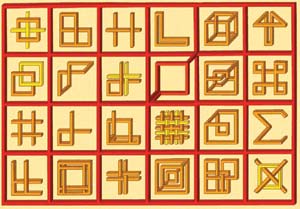
Невозможный алфавит - комбинация из возможных и невозможных фигур, среди которых есть даже элемент рамки.
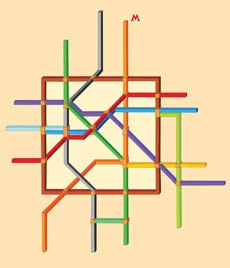
"Москва" (схема линий метрополитена)
Приложение 2.
Комната Амеса
И
зобретение
названо в честь реализовавшего его
Адельберта Амеса-младшего, офтальмолога
(США). Он впервые сконструировал свою
комнату в 1946 году. Данный дизайн создан
на основе представлений от Г.Гельмгольтца,
ведущих свое начало еще в 19-м веке.
В комнате Амеса представлены совместно две иллюзии. Первая - то, что комната выглядит кубической, хотя на самом деле она трапецеидальная, вторая заключается в том, что любые объекты смотрятся или увеличенными, или уменьшенными в зависимости от приближения/удаления от дальнего угла к ближнему.
Восприятие кубической комнаты
Если вы смотрите в комнату Амеса через смотровое отверстие (чтобы исключить ненужные точки просмотра), то данная комната кажется нормальной, то есть кубической, но этот образ обманчив. Пол, потолок, стены и дальние окна имеют форму трапеции. Например, дальний левый угол значительно ниже правого переднего. Стены смотрятся перпендикулярными полу, хотя на самом деле они не находятся под прямым углом по отношению к нему.
На схематическом рисунке показаны ощущения смотрящего и данность.
Основная форма - это действительная комната Амеса, пунктирные линии - линии света, форма, нарисованная пунктирно, - это то, какой вы ощущаете саму комнату Амеса. Причем два видимых угла комнаты смотрятся практически равноудаленно от точки просмотра. Но по-настоящему левый видимый угол дальше правого почти в два раза.
Если смотреть в комнату Амеса с другой точки, то ощущение иллюзии исчезнет, то есть комната перестанет быть кубической и откроются все секреты.
Хотя стоит только внимательно присмотреться к представленной фотографии, и элемент трапецеидальности можно найти. Но... На этом и держатся многие современные технологии, а также всевозможные технологии индустрии шоу-бизнеса - стереотипы:).
Практическое применение
Дело в том, что комната Амеса моделируема в современных условиях. Причем сие действие вполне под силу компьютерному дизайнеру. Не тому, кто сидит дома и изучает Photoshop, а тому, чья работа напрямую связана с Blue Box, с так называемой "голубой комнатой", в которой все действующие персонажи снимаются на голубом фоне, после чего оный вырезается и заменяется на компьютерный пейзаж (кстати, есть и Green Box). Так вот, помимо стандартных пейзажей, можно применить и комнату Амеса. Эффект будет превосходен, если создать компьютерное окружение, отталкиваясь от точки просмотра. Хотя это только в теории…
christopher@tut.by