Логика пространства
Рис. 16 Куб с полосками |
Под "логикой" пространства мы понимаем те отношения между физическими объектами, которые обычны для реального мира, и при нарушении которых возникают визуальные парадоксы, называемые еще оптическими иллюзиями. Большинство художников, экспериментирующие с логикой пространства, изменяют эти отношения между объектами, основываясь на своей интуиции, как, например, Пикассо.
Рис. 17 Сверху и снизу |
Эшер понимал, что геометрия определяет логику пространства, но и логика пространства определяет геометрию. Одна из наиболее часто используемый особенностей логики пространства - игра света и тени на выпуклых и вогнутых объектах. На литографии "Куб с полосками" (рис. 16) выступы на лентах являются визуальным ориентиром того, как расположены полоски в пространстве и как они переплетаются с кубом. И если вы верите своим глазам, то вы никогда не поверите тому, что нарисовано на этой картине.
Еще один из аспектов логики пространства - перспектива. На рисунках, в которых присутствует эффект перспективы, выделяют так называемые точки исчезновения, которые сообщают глазу человека о бесконечности пространства.
Вводя дополнительные точки исчезновения и немного изменяя элементы композиции для достижения нужного эффекта, Эшер смог изобразить картины, в которых изменяется ориентация элементов в зависимости от того, как зритель смотрит на картину. На картине "Cверху и cнизу" художник разместил сразу пять точек исчезновения - по углам картины и в центре. В результате, если мы смотрим на нижнюю часть картины, то создается впечатление, что мы смотрим вверх. Если же обратить взгляд на верхнюю половину картину, то кажется, что мы смотрим вниз. Чтобы подчеркнуть этот эффект, Эшер изобразил два вида одной и той же композиции.
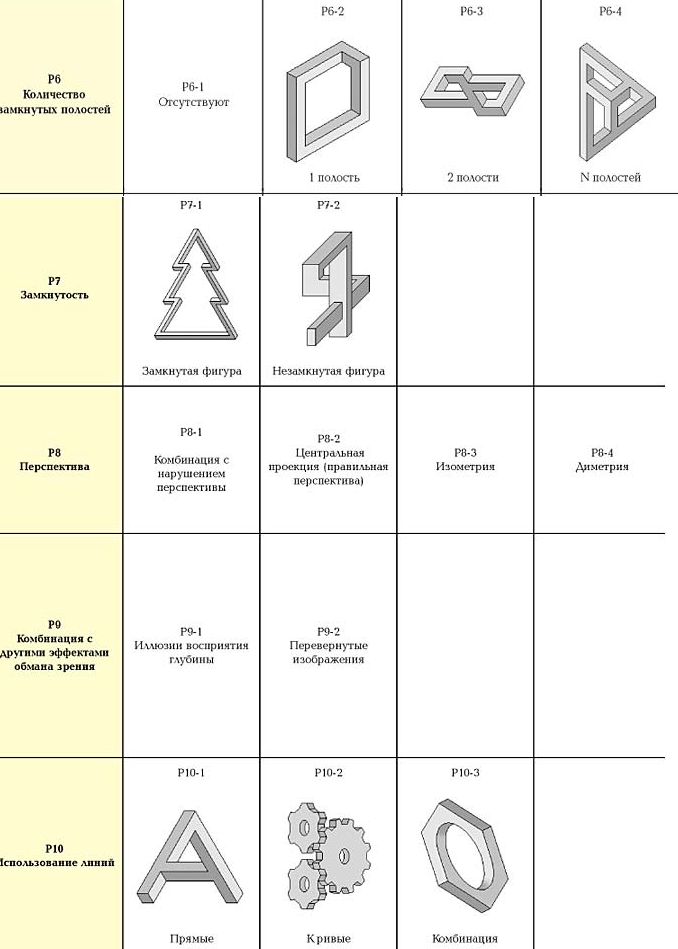
Классификация невозможных фигур
В ниже приведенной морфологической таблице классификации невозможных объектов можно найти основные типы невозможных фигур.
Таблица 1.
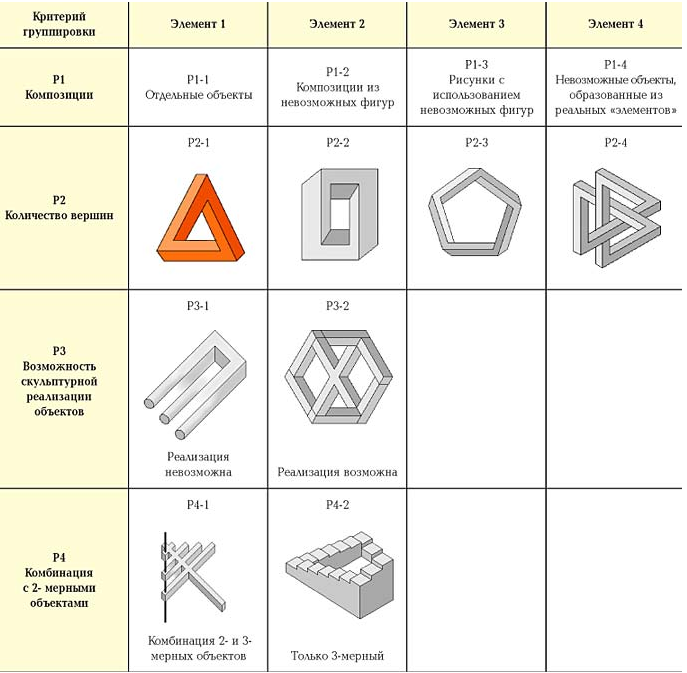
Таблица не претендует на полноту и строгий порядок, но дает возможность оценить все многообразие невозможных фигур. В таблице более 300 тысяч комбинаций различных элементов.
Заключение Создавайте сами невозможные объекты
Есть ли какая-либо более существенная польза от невозможных рисунков, чем игра ума? В некоторых больницах специально развешивают изображения невозможных объектов, поскольку их рассматривание способно надолго занять больных. Логично было бы развесить такие рисунки в кассах, в милиции и прочих местах, где ожидание своей очереди длится порой целую вечность. Рисунки могли бы выступить в роли этаких «хронофагов», т.е. пожирателей времени.
Рис. 18 |
Вообще математики легко оперируют с четырех-, пяти– и еще более многомерными объектами, однако изобразить их в трехмерном пространстве невозможно. «Октакуб», как и все подобные фигуры не является действительно четырехмерным. Его можно сравнить с картой – проекцией трехмерной поверхности земного шара на плоский лист бумаги.
Трехмерная проекция четырехмерной фигуры была получена Окнеану методом радиальной стереографии при помощи компьютера. При этом была сохранена симметрия исходной четырехмерной фигуры. Скульптура имеет 24 вершины и 96 граней. В четырехмерным пространстве грани фигуры прямые, но в проекции они искривлены. Углы же между гранями у трехмерной проекции и исходной фигуры одинаковы.
«Октакуб» был изготовлен из нержавеющей стали в инженерных мастерских Университета штата Пенсильвания. Установлена скульптура в отремонтированном корпусе имени Макаллистера математического факультета. Высота, ширина и длина скульптуры одинаковы и составляют около 180 см. Размещена скульптура на гранитном пьедестале высотой 90 см так, чтобы е центр находился примерно на уровне взгляда человека.
В наше время, смотря на множество конструированых всевозможных фигур и на то, что создано моими во всем мире, могжно назвать это робким началом чего-то более значительного и всеобъемлющего. Поэтому в ближайшем будущем можно ожидать, что игра со зрительным восприятием реализуется в области голограмм и изображений, созданных компьютером. Может быть, уже к концу нашего столетия будет воздвигнут храм невозможного, в котором нам откроется головокружительная перспектива прекрасного и достойного поклонения несуществующего, освобождающего нас на несколько мгновений от цепей реальности.
Собственно говоря, невозможный объект несложно создать. Если вы знаете обычные геометрические фигуры и у вас есть немного воображения, то это можно сделать за считанные минуты. Поскольку создание невозможных объектов довольно сильно ограничено пределами графики, вполне возможно, что два человека, работающие независимо друг от друга, могут создать что-то одинаковое или очень похожее. Вдохновить на создание невозможных объектов может практически все. (см. приложение 2) При создании фигур, которые мы видим в моей работе в качестве образцов использовались обыкновенные бытовые предметы и некоторые более-менее знакомые вещи. Они были по-новому переосмыслены, преображены и доведены до совершенства всего лишь при помощи воображения. Находить невозможные объекты в обыкновенных предметах так же увлекательно, как и искать сокровища. Из простых рисунков может родиться огромное количество невозможных объектов. Еще более интересно – самому дать им названия! Возможно, лучший способ начать – взять в руки блокнот и карандаш, сделать несколько набросков знакомых предметов, с которыми встречаешься ежедневно. Не берите ничего сложного, лучше используйте фигуры с простой геометрической формой. Нарисовав что-то, попытайтесь поэкспериментировать, сделав несколько последовательных рисунков. В этом надо немного попрактиковаться, но вы будете удивлены конечным результатом. Ваше задание (уж вам решать, принимать его или нет) состоит в том, чтобы создать собственный невозможный объект в домашних условиях!