35. Эквивалентные бесконечно малые. Сравнение бесконечно малых.

Функция   называется бесконечно малой при   (или в точке   ), если 

Подробная теория про бесконечно малые функции по ссылке.

Пример

Функция   является б.м. при  , так как

Бесконечно малые функции одного порядка

Пусть   и   - две б.м. функции при  .

Определение

Функции   и   называются б.м. одного порядка малости при  , если 

Пример

Рассмотрим функции   и  , которые являются б.м. при  :

Найдем предел отношения этих функций при  :

Так как предел равен конечному, отличному от нуля числу, то рассматриваемые функции   и  являются б.м. одного порядка малости при  .

Бесконечно малые функции более низкого и высокого порядков

Определение

Если  , то   является б.м. более высокого порядка при  , чем  , а   - б.м. более низкого порядка по сравнению с  :   при  .

Пример

Функция   ,   является б.м. более высокого порядка, чем функция   ,   в точке  , так как

Определение

Если  , то   - б.м. низшего порядка малости при   по сравнению с  .

Пример

Рассмотрим функцию  , которая является б.м. в точке  : , и б.м. в этой же точке функцию  : . Найдем предел частного этих функций:

А поэтому, функция   является б.м. низшего порядка малости при  , чем функция  .

Определение

Если  , то   называется б.м. порядка   по сравнению с   при .

Пример

Функция   называется б.м. порядка 2 по сравнению с функцией   в точке , так как

, что и требовалось доказать.

Эквивалентные (равносильные) бесконечно малые функции

Определение

Если  , то б.м. функции   и   называются эквивалентными или равносильными б.м. одного порядка при  :   при  .

Пример

Функции   и   являются эквивалентными б.м. в точке  , так как, во-первых:

а во-вторых:

36. Непрерывность функции в точке. Три определения непрерывности.

ОПРЕДЕЛЕНИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ

Мы повторим здесь определение непрерывности функции, данное выше, в главе о пределах.

        Определение 3.1   Пусть функция   определена на некотором интервале  , для которого   -- внутренняя точка. Функция   называется непрерывной в точке  , если существует предел   при   и этот предел равен значению  , то есть

Пусть функция   определена на некотором полуинтервале  , для которого   -- левый конец. Функция   называется непрерывной справа в точке  , если существует предел  при   и этот предел равен значению  , то есть

Пусть, наконец, функция   определена на некотором полуинтервале  , для которого   -- правый конец. Функция   называется непрерывной слева в точке  , если существует предел   при   и этот предел равен значению  , то есть

    

Из теоремы о связи двустороннего предела с односторонними (теорема 2.1) сразу следует, как уже отмечалось в главе 2, что имеет место следующее предложение.

        Предложение 3.1   Функция   тогда и только тогда непрерывна в точке  , когда она непрерывна в точке   справа и слева, то есть когда выполнены следующие условия:

1) функция   определена в точке   и в некоторой окрестности этой точки;

2) существует предел значений функции слева:  ;

3) существует предел значений функции справа:  ;

4) эти два предела совпадают между собой и со значением функции в точке  :  .     

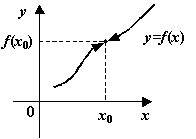
Рис.3.1.Функция непрерывна: пределы слева и справа совпадают с 

Точка  , в которой функция непрерывна, называется точкой непрерывности функции  ; так же определяются точки непрерывности слева и справа.

        Пример 3.1   Пусть   и  . Тогда   и  . Эти значения совпадают, значит, функция   непрерывна в точке  .

(Функция   -- элементарная функция;   -- точка её области определения  . Все элементарные функции непрерывны во всех внутренних точках своих областей определения, в том числе и эта.Так что в этом примере можно было бы заменить   любой элементарной функцией, а   -- любой внутренней точкой области  , и вывод остался бы тем же.)     

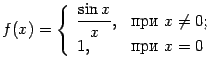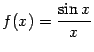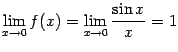        Пример 3.2   Рассмотрим функцию   и точку  . При   функция задаётся формулой  , при этом имеем  (первый замечательный предел). Это значение совпадает с тем, которое задано при  :  . Итак,  , что означает непрервыность функции   при  .     

Тем, кто внимательно изучил данное в главе 2 общее понятие базы предела, можно предложить продумать и доказать следующее утверждение:

        Предложение 3.2   Пусть   -- база непроколотых окрестностей точки  , окончаниями которой служат интервалы  ,  ;   -- база непроколотых левых окрестностей точки  , окончаниями которой служат полуинтервалы  ,  ;   -- база непроколотых правых окрестностей точки  , окончаниями которой служат полуинтервалы  ,  . Тогда непрерывность функции   в точке   эквивалентна тому, что существует предел  ; непрерывность слева в точке   -- тому, что существует предел  ; непрерывность справа в точке   -- тому, что существует предел  .