Основные неопределенности пределов и их раскрытие.
С непосредственным вычислением пределов основных элементарных функций разобрались.
При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называютнеопределенностями.
Перечислим
все основные
виды неопределенностей:
ноль делить на ноль 
(0
на 0),
бесконечность делить на бесконечность 
,
ноль умножить на бесконечность 
,
бесконечность минус бесконечность 
,
единица в степени бесконечность 
,
ноль в степени ноль 
,
бесконечность в степени ноль 
.
ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.
Раскрывать неопределенности позволяет:
упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);
использование замечательных пределов;
применение правила Лопиталя;
использование замены бесконечно малого выражения ему эквивалентным(использование таблицы эквивалентных бесконечно малых).
Сгруппируем неопределенности в таблицу неопределенностей. Каждому виду неопределенности поставим в соответствие метод ее раскрытия (метод нахождения предела).
Эта таблица вместе с таблицей пределов основных элементарных функций будут Вашими главными инструментами при нахождении любых пределов.
34. Второй замечательный предел. Три формы записи второго замечательного предела.
Второй
замечательный предел имеет
вид:
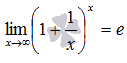
или
в другой записи
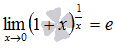
В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность .
Разберем несколько примеров нахождения предела по второму замечательному пределу сподробнымоприсанием решения.
Пример.
Вычислить
предел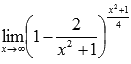 
Решение.
Подставляем
бесконечность:
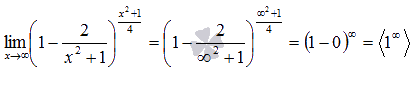
Пришли к неопределенности единица в степени бесконечность. Смотрим в таблицу неопределенностей для определения метода решения и останавливаемся на применении второго замечательного предела.
Сделаем
замену переменных. Пусть
Если 
,
то 
Исходный
предел после замены примет вид:
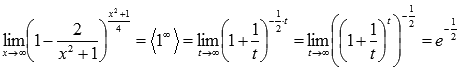
Ответ:
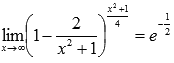
Пример.
Вычислить
предел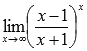 
Решение.
Подставляем
бесконечность:
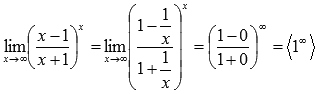
Пришли
к неопределенности единица в степени
бесконечность, которая указывает на
применение второго замечательного
предела. Выделим целую часть в основании
показательно степенной функции:
Тогда
предел запишется в виде:
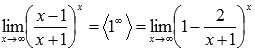
Сделаем
замену переменных. Пусть
Если
,
то 
Исходный
предел после замены примет вид:
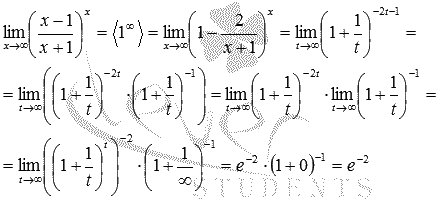
В преобразованиях были использованы свойства степени и свойства пределов.
Ответ:
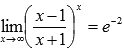
Пример.
Вычислить
предел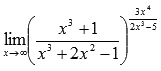 
Решение.
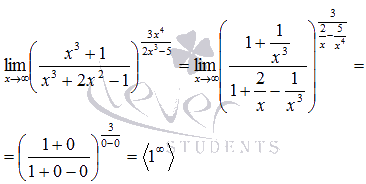
Преобразуем
функцию, чтобы применить второй
замечательный предел:
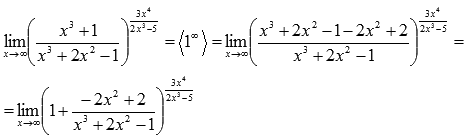
Сейчас
домножим показатель на 
и
разделим на это же выражение, затем
используем свойства степени:
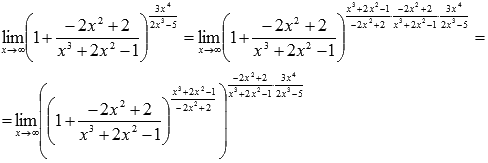
Так
как показатели степени числителя и
знаменателя дроби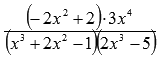 
одинаковые
(они равны 6),
то предел этой дроби на бесконечности
равен отношению коэффициентов при
старших степенях (см.
непосредственное вычисление пределов):
Если
произвести замену 
,
то получим второй замечательный предел
в чистом виде, следовательно,
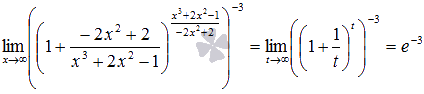
Ответ:
