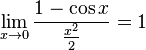- •Матрицы.Действия с матрицами
- •3.Миноры и алгебраические дополнения.Обратная матрица
- •1) Если система (2.3) имеет единственное решение, определяемое по формулам: .
- •7. Векторы. Действия с векторам. Коллиниарность векторов
- •8.Линейная зависимость векторов
- •10. Понятие базис.Разложение вектора по базису.
- •11.Декартовая система координат. Направление косинуса вектора.
- •12. Скалярное произведение векторов. Необходимое и достаточное условие.
- •13.Векторное произведение. Необходимое и достаточное условие векторов.
- •14. Смешанное произведение векторов. Компланарность векторов.
- •15. Плоскость в пространстве. Основные уравнения плоскости.
- •17. Прямая в пространстве. Различные уравнения прямой
- •18. Переход от общего уравнения прямой к кононическому.
- •19. Взаимное расположение прямой в пространстве
- •20. Прямая на плоскости. Различные формы уравнений прямой на плоскости.
- •21. Расстояние от произвольной точки до прямой на плоскости. Условия параллельности и перпендикулярности прямых на плоскости.
- •22. Каноническое уравнение прямых второго порядка. Элипс, гипербола, парабола
- •Классификация кривых второго порядка[править | править исходный текст] Невырожденные кривые[править | править исходный текст]
- •Вырожденные кривые[править | править исходный текст]
- •23. Преобразование координат на плоскости. Приведение общего уравнения кривой второго порядка у каноническому виду Преобразование декартовых прямоугольных координат на плоскости
- •24.Множества. Действительные числа. Логически символы. Окрестность точки
- •2. Операции над множествами
- •25. Числовые последовательности. Предел числовой последовательности. Теорема вейерштрасса.
- •26. Определение функции. Способы задания функции. Основные характеристики функций. Элементарные функции.
- •27. Предел функции в точке.
- •Свойства пределов числовых функций[править | править исходный текст]
- •28.Предел функции при X→∞. Односторонние пределы.
- •29. Бесконечно малые и бесконечно большие функции. Свойства бесконечно малые и бесконечно большие функций.
- •30. Связь бесконечно малых и бесконечно больших. Их свойства.
- •31. Теорема о связи между функцией, ее пределом и бесконечно малой величиной.
- •32. Признак существования предела функции. Первый замечательный предел. Первый замечательный предел
- •33. Основные свойства пределов функций. Основные типы неопределенностей.
- •Основные неопределенности пределов и их раскрытие.
- •34. Второй замечательный предел. Три формы записи второго замечательного предела.
- •35. Эквивалентные бесконечно малые. Сравнение бесконечно малых.
- •36. Непрерывность функции в точке. Три определения непрерывности.
- •37. Точки разрыва функции и их классификация
- •38. Основные теоремы о непрерывных функциях.
- •39. Свойства функций непрерывных на отрезке. Геометрическая интерпретация этих свойств.
32. Признак существования предела функции. Первый замечательный предел. Первый замечательный предел
![]()
Доказательство
Рассмотрим односторонние
п
 ределы
ределы ![]() и
и ![]() и
докажем, что они равны 1.
и
докажем, что они равны 1.
Пусть ![]() .
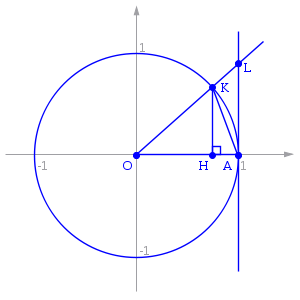
Отложим этот угол на единичной окружности
(R =
1).
.
Отложим этот угол на единичной окружности
(R =
1).
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.
Очевидно, что:
![]() (1)
(1)
(где SsectOKA — площадь сектора OKA)
![]()
![]()
![]()
(из ![]() :
| LA |
= tgx)
:
| LA |
= tgx)
Подставляя в (1), получим:
![]()
Так
как при ![]() :
:
![]()
Умножаем на sinx:
![]()
Перейдём к пределу:
![]()
![]()
![]()
Найдём левый односторонний предел:
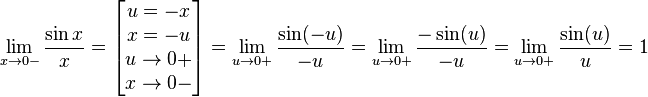
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
Доказательство следствий
![]()
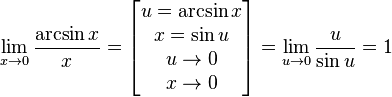
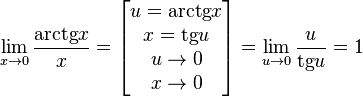
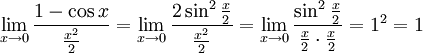

33. Основные свойства пределов функций. Основные типы неопределенностей.
Определение и свойства пределов |
||||||||||||||
Число b называется пределом функции f(x) при x → a, если для любого ε > 0 сущестувует δ > 0 такое, что для любого x из δ-окрестности a (|x - a| < δ) выполняется |f(x) - f(a)| < ε. |
||||||||||||||
Запись: ∀ ε > 0 ∃ δ > 0 : |x - a| < δ => |f(x) - f(a)| < ε |
||||||||||||||
Обозначение |
||||||||||||||
|
||||||||||||||
Свойства пределов |
||||||||||||||
|
||||||||||||||
|
||||||||||||||
|
||||||||||||||
|
||||||||||||||
Замечательные пределы |
||||||||||||||
|
||||||||||||||
|
||||||||||||||
e = 2,718281828459045235360287471352662497757... |
||||||||||||||
Связь между десятичными и натуральными логарифмами |
||||||||||||||
lg(x) = M ln(x), |
||||||||||||||
где M = lg(e) = 0,43429448190325182765112891891666... |