
- •Матрицы.Действия с матрицами
- •3.Миноры и алгебраические дополнения.Обратная матрица
- •1) Если система (2.3) имеет единственное решение, определяемое по формулам: .
- •7. Векторы. Действия с векторам. Коллиниарность векторов
- •8.Линейная зависимость векторов
- •10. Понятие базис.Разложение вектора по базису.
- •11.Декартовая система координат. Направление косинуса вектора.
- •12. Скалярное произведение векторов. Необходимое и достаточное условие.
- •13.Векторное произведение. Необходимое и достаточное условие векторов.
- •14. Смешанное произведение векторов. Компланарность векторов.
- •15. Плоскость в пространстве. Основные уравнения плоскости.
- •17. Прямая в пространстве. Различные уравнения прямой
- •18. Переход от общего уравнения прямой к кононическому.
- •19. Взаимное расположение прямой в пространстве
- •20. Прямая на плоскости. Различные формы уравнений прямой на плоскости.
- •21. Расстояние от произвольной точки до прямой на плоскости. Условия параллельности и перпендикулярности прямых на плоскости.
- •22. Каноническое уравнение прямых второго порядка. Элипс, гипербола, парабола
- •Классификация кривых второго порядка[править | править исходный текст] Невырожденные кривые[править | править исходный текст]
- •Вырожденные кривые[править | править исходный текст]
- •23. Преобразование координат на плоскости. Приведение общего уравнения кривой второго порядка у каноническому виду Преобразование декартовых прямоугольных координат на плоскости
- •24.Множества. Действительные числа. Логически символы. Окрестность точки
- •2. Операции над множествами
- •25. Числовые последовательности. Предел числовой последовательности. Теорема вейерштрасса.
- •26. Определение функции. Способы задания функции. Основные характеристики функций. Элементарные функции.
- •27. Предел функции в точке.
- •Свойства пределов числовых функций[править | править исходный текст]
- •28.Предел функции при X→∞. Односторонние пределы.
- •29. Бесконечно малые и бесконечно большие функции. Свойства бесконечно малые и бесконечно большие функций.
- •30. Связь бесконечно малых и бесконечно больших. Их свойства.
- •31. Теорема о связи между функцией, ее пределом и бесконечно малой величиной.
- •32. Признак существования предела функции. Первый замечательный предел. Первый замечательный предел
- •33. Основные свойства пределов функций. Основные типы неопределенностей.
- •Основные неопределенности пределов и их раскрытие.
- •34. Второй замечательный предел. Три формы записи второго замечательного предела.
- •35. Эквивалентные бесконечно малые. Сравнение бесконечно малых.
- •36. Непрерывность функции в точке. Три определения непрерывности.
- •37. Точки разрыва функции и их классификация
- •38. Основные теоремы о непрерывных функциях.
- •39. Свойства функций непрерывных на отрезке. Геометрическая интерпретация этих свойств.
30. Связь бесконечно малых и бесконечно больших. Их свойства.
Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.
Доказательство. Возьмем
произвольное число ε>0 и
покажем, что при некотором δ>0 (зависящим
от ε) при всех x,
для которых |x
– a|<δ,
выполняется неравенство ![]() ,
а это и будет означать, что 1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) –
бесконечно большая функция при x→a,
то найдется δ>0 такое,
что как только |x
– a|<δ,
так |f(x)|>1/ ε.
Но тогда для тех же x
.
,
а это и будет означать, что 1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) –
бесконечно большая функция при x→a,
то найдется δ>0 такое,
что как только |x
– a|<δ,
так |f(x)|>1/ ε.
Но тогда для тех же x
.
Примеры.
Ясно, что при x→+∞ функция y=x2+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция
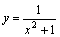 –
бесконечно малая при x→+∞,
т.е.
–
бесконечно малая при x→+∞,
т.е. 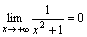 .
.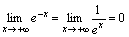 .
.
Можно доказать и обратную теорему.
Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.
Доказательство теоремы проведите самостоятельно.
Примеры.
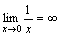 .
.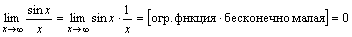 .
.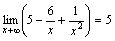 ,
так как функции
,
так как функции 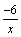 и
и 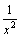 -
бесконечно малые при x→+∞,
то
-
бесконечно малые при x→+∞,
то 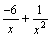 ,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же 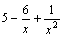 является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0
![]() .
.
31. Теорема о связи между функцией, ее пределом и бесконечно малой величиной.
ОПРЕДЕЛЕНИЕ БЕСКОНЕЧНО МАЛОЙ И БЕСКОНЕЧНО БОЛЬШОЙ ФУНКЦИЙ. СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ. ТЕОРЕМА О СВЯЗИ МЕЖДУ БЕСКОНЕЧНО БОЛЬШОЙ И БЕСКОНЕЧНО МАЛОЙ ФУНКЦИЯМИ.
Функция ![]() называется бесконечно
малой при
называется бесконечно
малой при ![]() ,
если
,
если![]() .
.
Функция
называется бесконечно
большой при
,
если для любого положительного
числа ![]() существует
такое число
существует
такое число ![]() ,
что для всех
,
что для всех ![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() .
Записывается:
.
Записывается: ![]() .
.
Свойства бесконечно малых функций:
1)Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
2)Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
3)Произведение двух бесконечно малых функций есть функция бесконечно малая.
4)Произведение бесконечно малой функции на число есть функция бесконечно малая.
5)Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
Теорема о связи между бесконечно большой и бесконечно малой функциями:
Если
функция ![]() -
функция бесконечно малая (
-
функция бесконечно малая (![]() ),
то функция
),
то функция ![]() есть
бесконечно большая функция и наоборот.
есть
бесконечно большая функция и наоборот.
Доказательство:
Пусть
-
бесконечно малая функция при
,
т.е. ![]() .
Тогда для любого числа
.
Тогда для любого числа ![]() существует
такое число
существует
такое число ![]() ,
что для всех
,
удовлетворяющих неравенству
,
выполняется неравенство
,
что для всех
,
удовлетворяющих неравенству
,
выполняется неравенство ![]() ,
т.е.
,
т.е. ![]() ,
т.е.
,
т.е. ![]() ,
где
,
где ![]() .
А из этого следует, что функция
.
А из этого следует, что функция ![]() -
бесконечно большая.
-
бесконечно большая.
