Классификация кривых второго порядка[править | править исходный текст] Невырожденные кривые[править | править исходный текст]

Кривая второго порядка называется невырожденной, если   Могут возникать следующие варианты:

• Невырожденная кривая второго порядка называется центральной, если 

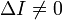
  • эллипс — при услови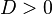и   и  ;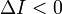

    • частный случай эллипса — окружность — при услови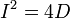и   или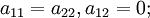 

  • мнимый эллипс (ни одной вещественной точки) — при условии 

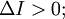
  • гипербола — при условии 

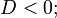
• Невырожденная кривая второго порядка называется нецентральной, если 

  • парабола — при условии 

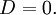
Вырожденные кривые[править | править исходный текст]

Кривая второго порядка называется вырожденной, если  . Могут возникать следующие варианты:

• вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии 

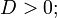
• пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии 

• вырожденная парабола — при условии 

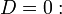
  • пара вещественных параллельных прямых — при условии 

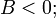
  • одна вещественная прямая (две слившиеся параллельные прямые) — при условии 

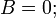
  • пара мнимых параллельных прямых (ни одной вещественной точки) — при условии 

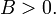
23. Преобразование координат на плоскости. Приведение общего уравнения кривой второго порядка у каноническому виду Преобразование декартовых прямоугольных координат на плоскости

     Параллельный сдвиг координатных осей (рис. 4.8) 

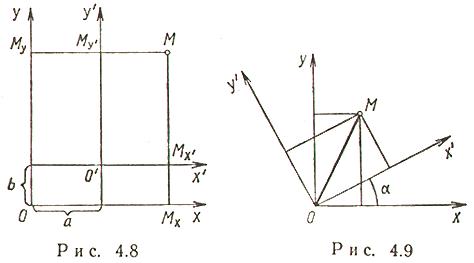
     Поворот координатных осей (рис. 4.9) 

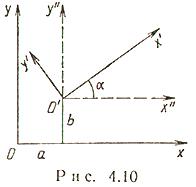
     Параллельный сдвиг и поворот координат осей (рис. 4.10) 

Пусть в прямоугольной системе координат   алгебраическая линия второго порядка задана уравнением (3.34):

Чтобы привести уравнение к каноническому виду, нужно выполнить следующие действия.

1. Если в уравнении имеется член с произведением неизвестных  , то делаем поворот системы координат:

на угол  , удовлетворяющий равенству  . При этом получим "почти" приведенное уравнение линии второго порядка:

Если  , переходим к пункту 2, поворот системы координат делать не нужно, так как исходное уравнение имеет "почти" приведенный вид.

2. Выполняем параллельный перенос системы координат:

а) если в уравнении нет линейных членов, то переходим к пункту 3;

б) если в уравнении имеется линейный член с какой-либо неизвестной и квадратичный член с этой же неизвестной, то, дополняя эти члены до полного квадрата, делаем замену, чтобы в уравнении не стало линейного члена с этой неизвестной. Например, если в уравнении   и  ,то выполняем преобразования:

а затем замену неизвестных  , после которой в уравнении не будет линейного члена с неизвестной  ;

в) если в уравнении имеется только один линейный член с какой-либо неизвестной, а квадрат этой неизвестной отсутствует, то при помощи замены этой переменной надо сделать равным нулю свободный член уравнения. Например, если уравнение имеет вид

то, выполняя замену неизвестных  , получаем уравнение без свободного члена:

3. Полученное в результате упрощений (пункт 2) уравнение имеет "почти" канонический вид. Для окончательного упрощения "почти" канонического уравнения при необходимости применяются следующие преобразования:

а) переименование координатных осей:  ;

б) изменение направления координатной оси, например оси абсцисс:  ;

в) умножение обеих частей уравнения на отличный от нуля множитель;

г) перенос членов из одной части уравнения в другую.

В результате этих преобразований уравнение приводится к каноническому виду. Замену неизвестных, приводящую уравнение поверхности к каноническому виду, определяем как композицию всех замен, применяемых в ходе решения.

Пример 3.19. В прямоугольной системе координат   заданы уравнения алгебраических линий второго порядка:

а)  ;

б)  ;

в)  ;

г)  .

Каждое уравнение привести к каноническому виду. Указать связь между исходной и канонической системами координат.

Решение.

а) Сравнивая заданное уравнение с общим уравнением (3.34), находим коэффициенты

1. Поскольку  , поворот системы координат делать не нужно.

2. В уравнении имеются квадраты обеих неизвестных. Преобразуем левую часть заданного уравнения, выделяя полные квадраты:

Следовательно, уравнение можно записать в виде  . Делая замену  или, выражая старые координаты через новые:  , получаем   — каноническое уравнение пары пересекающихся прямых (см. уравнение (5) в теореме 3.3 при  ). В данном случае пункта 3 алгоритма не выполняется.

б) Сравнивая заданное уравнение с общим уравнением (3.34), находим коэффициенты

1. Поскольку в заданном уравнении нет произведения неизвестных  , то уравнение имеет "почти" приведенный вид.

2. Выделяя полный квадрат по неизвестной  , получаем

Делая замену   или, выражая старые координаты через новые:  получаем   — каноническое уравнение параболы (см. уравнение (6) в теореме 3.3 при  ).

в) Сравнивая заданное уравнение с общим уравнением (3.34), находим коэффициенты

1. В заданном уравнении имеется произведение неизвестных  , поэтому необходимо сделать поворот системы координат. Величину   угла поворота находим по формуле (3.40):

то есть  , учитывая ограничение  . При повороте системы координат на угол   старые координаты выражаются через новые по формулам (3.35):

Подставляя их в левую часть заданного уравнения, получаем

Раскрываем скобки и приводим подобные члены:

2. Так как линейные члены отсутствуют, то параллельный перенос системы координат делать не нужно.

3. Переносим свободный член в правую часть и делим обе части уравнения на (-8):

Осталось поменять названия координатных осей, т.е. сделать замену   после которой получаем   — каноническое уравнение гиперболы (см. уравнение (4) в теореме 3.3 при  ). Найдем формулы перехода от исходной системы координат   к канонической  . Подставляя   в формулы поворота на угол  , получаем

г) Сравнивая заданное уравнение с общим уравнением (3.34), находим коэффициенты

1. В заданном уравнении имеется произведение неизвестных  , поэтому необходимо сделать поворот системы координат. Величину  угла поворота находим по формуле (3.40):

Так как  , то из уравнения   находим тангенс искомого угла:

 или 

Ограничению   удовлетворяет острый угол  . Вычисляем   и   и делаем замену:

соответствующую повороту (3.35) на угол  . Получаем уравнение

Раскрываем скобки и приводим подобные члены:

Получили приведенное уравнение (III).

2. "Уничтожаем" линейные члены, выделяя полные квадраты:

После замены   или, выражая старые координаты через новые:  получаем  .

3. Переносим свободный член в правую часть и делим обе части уравнения на 100:

Это уравнение похоже на каноническое уравнение эллипса (см. уравнение (1) в теореме 3.3 при   и  ). Однако, его коэффициенты не удовлетворяют неравенству  . Поэтому необходимо переименовать координатные оси, т.е. сделать замену   после которой получаем каноническое уравнение эллипса  .

Формулы перехода от исходной системы координат   к канонической получаем как композицию преобразований прямоугольных координат,

выражения параллельного переноса   а затем — отражения   Первая подстановка дает:

вторая подстановка дает искомую связь