
- •Матрицы.Действия с матрицами
- •3.Миноры и алгебраические дополнения.Обратная матрица
- •1) Если система (2.3) имеет единственное решение, определяемое по формулам: .
- •7. Векторы. Действия с векторам. Коллиниарность векторов
- •8.Линейная зависимость векторов
- •10. Понятие базис.Разложение вектора по базису.
- •11.Декартовая система координат. Направление косинуса вектора.
- •12. Скалярное произведение векторов. Необходимое и достаточное условие.
- •13.Векторное произведение. Необходимое и достаточное условие векторов.
- •14. Смешанное произведение векторов. Компланарность векторов.
- •15. Плоскость в пространстве. Основные уравнения плоскости.
- •17. Прямая в пространстве. Различные уравнения прямой
- •18. Переход от общего уравнения прямой к кононическому.
- •19. Взаимное расположение прямой в пространстве
- •20. Прямая на плоскости. Различные формы уравнений прямой на плоскости.
- •21. Расстояние от произвольной точки до прямой на плоскости. Условия параллельности и перпендикулярности прямых на плоскости.
- •22. Каноническое уравнение прямых второго порядка. Элипс, гипербола, парабола
- •Классификация кривых второго порядка[править | править исходный текст] Невырожденные кривые[править | править исходный текст]
- •Вырожденные кривые[править | править исходный текст]
- •23. Преобразование координат на плоскости. Приведение общего уравнения кривой второго порядка у каноническому виду Преобразование декартовых прямоугольных координат на плоскости
- •24.Множества. Действительные числа. Логически символы. Окрестность точки
- •2. Операции над множествами
- •25. Числовые последовательности. Предел числовой последовательности. Теорема вейерштрасса.
- •26. Определение функции. Способы задания функции. Основные характеристики функций. Элементарные функции.
- •27. Предел функции в точке.
- •Свойства пределов числовых функций[править | править исходный текст]
- •28.Предел функции при X→∞. Односторонние пределы.
- •29. Бесконечно малые и бесконечно большие функции. Свойства бесконечно малые и бесконечно большие функций.
- •30. Связь бесконечно малых и бесконечно больших. Их свойства.
- •31. Теорема о связи между функцией, ее пределом и бесконечно малой величиной.
- •32. Признак существования предела функции. Первый замечательный предел. Первый замечательный предел
- •33. Основные свойства пределов функций. Основные типы неопределенностей.
- •Основные неопределенности пределов и их раскрытие.
- •34. Второй замечательный предел. Три формы записи второго замечательного предела.
- •35. Эквивалентные бесконечно малые. Сравнение бесконечно малых.
- •36. Непрерывность функции в точке. Три определения непрерывности.
- •37. Точки разрыва функции и их классификация
- •38. Основные теоремы о непрерывных функциях.
- •39. Свойства функций непрерывных на отрезке. Геометрическая интерпретация этих свойств.
18. Переход от общего уравнения прямой к кононическому.
Переход от общих уравнений прямой к каноническим или параметрическим уравнениям
|
Для того, чтобы от общих уравнений
каноническим или параметрическим уравнениям прямой,
требуется
найти направляющий вектор
прямой
и координаты любой точки принадлежащей ей. Направляющий вектор прямой ортогонален
нормалям
к
обеим плоскостям, следовательно, коллинеарен их векторному произведению
направляющего
вектора можно выбрать или любой вектор с пропорциональными координатами. Чтобы найти точку, лежащую на данной прямой, можно задать одну ее координату произвольно, а две остальные
найти из уравнений , выбрав их так, чтобы определитель из их коэффициентов не равнялся нулю. |
Пример.
Составить канонические и параметрические
уравнения прямой ![]() .
.
Решение.
По условию ![]() ,
, ![]() тогда
тогда ![]() .
Следовательно, направляющим вектором
прямой можно считать вектор
.
Следовательно, направляющим вектором
прямой можно считать вектор ![]() .
.
Будем
искать точку на прямой с координатой ![]() .
Для координат
.
Для координат ![]() и
и ![]() получим
систему уравнений
получим
систему уравнений ![]() ,
откуда
,
откуда ![]() ,
, ![]() .
Теперь можно составить канонические
уравнения прямой:
.
Теперь можно составить канонические
уравнения прямой:
![]() .
.
Параметрические уравнения той же прямой имеют вид:
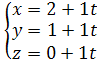 или
или 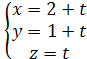 .
.
Пример.
Привести общие уравнения прямой ![]() к
каноническому виду.
к
каноническому виду.
Решение.
Найдём точку,
лежащую на прямой. Для этого выберем
произвольно одну из координат,
например, ![]() и
решив систему уравнений
и
решив систему уравнений ![]() найдем
найдем ![]() .
.
Нормальные
векторы плоскостей, определяющих
прямую, имеют координаты ![]() ,
, ![]() .
Поэтому направляющий вектор прямой
будет
.
Поэтому направляющий вектор прямой
будет ![]() .
Следовательно,
.
Следовательно, ![]() .
.
Замечание. Если какая-либо из координат направляющего вектора равна 0, то предполагается, что для любой точки прямой числитель соответствующей дроби в канонических уравнениях тоже равен 0.
Пусть
прямая перпендикулярна одной из
координатных осей, например оси ![]() .
Тогда направляющий вектор
прямой
перпендикулярен
.
Тогда направляющий вектор
прямой
перпендикулярен
,
следовательно, ![]() и
параметрические уравнения прямой
примут вид
и
параметрические уравнения прямой
примут вид 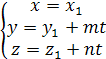 .
Исключаяиз уравнений параметр t,
получим уравнения прямой в виде
.
Исключаяиз уравнений параметр t,
получим уравнения прямой в виде 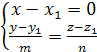 .
.
Однако,
и в этом случае, формально записывают
канонические уравнения прямой в виде ![]() .
.
Таким образом, если в знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Аналогично,
каноническим уравнениям ![]() соответствует
прямая перпендикулярная осям
и
соответствует
прямая перпендикулярная осям
и ![]() или
параллельная оси
или
параллельная оси ![]() .
.
Пример.
Записать уравнение прямой ![]() в параметрическом виде.
в параметрическом виде.
Решение.
Обозначим ![]() ,
отсюда
,
отсюда 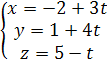
Пример.
Составить канонические и параметрические
уравнения прямой, проходящей через
точку ![]() параллельно
вектору
параллельно
вектору ![]() .
.
Решение.
Канонические уравнения: ![]() или
или ![]() .
.
Параметрические
уравнения:  или
или 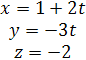 .
.


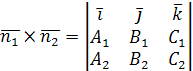 .
Поэтому в качестве
.
Поэтому в качестве