1. Матрицы.Действия с матрицами

Матрицей называется прямоугольная таблица чисел, состоящая из mодинаковой длины строк или n одинаковой длины стробцов.

aij- элемент матрицы, который находится в i-ой строке и j-м столбце.

Матрицей размерности m x n называется прямоугольная таблица m x n чисел a _ij , i=1,..., m, j=1,..., n:

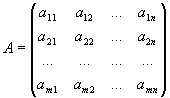
расположенных в m строках и n столбцах. Матрица называется квадратной, еслиm=n (n - порядок матрицы).

Линейные матричные операции По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы.  Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

Произведение матриц определяется следующим образом. Пусть заданы две матрицыA и B, причем число столбцов первой из них равно числу строк второй. Если

,  ,

то произведением матриц A и B, называется матрица

,

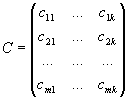элементы которой вычисляются по формуле

c _ij =a _i1 b _1j + a _i2 b _2j + ... +a _in b _nj , i=1, ..., m, j=1, ..., k.

Произведение матриц A и B обозначается AB, т.е. C=AB.

 

ПРИМЕР 1. Действия с матрицами.

 

Произведение матриц, вообще говоря, зависит от порядка сомножителей. ЕслиAB=BA, то матрицы A и B называются перестановочными.

 

ПРИМЕР 2. Проверка перестановочности матриц.

 

Для квадратных матриц определена единичная матрица - квадратная матрица, все диагональные элементы которой единицы, а остальные - нули: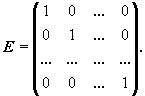

Единичная матрица чаще всего обозначается буквой E или E _n, где n - порядок матрицы. Непосредственным вычислением легко проверить основное свойствоединичной матрицы:

AE=EA=A.

Скалярной матрицей называется диагональная матрица с одинаковыми числами на главной диагонали; единичная матрица - частный случай скалярной матрицы.

ПРИМЕР 3. Умножение матрицы на матрицы специального вида

Для квадратных матриц определена операция возведения в целую неотрицательную степень:

A ⁰ =E, A ¹ =A, A ² =AA, ..., A ⁿ =A ^n-1 A, ....

 

ПРИМЕР 4. Возведение матрицы в степень.

 

Для прямоугольных матриц определена операция транспонирования. Рассмотрим произвольную прямоугольную матрицу A. Матрица, получающаяся из матрицы Aзаменой строк столбцами, называется транспонированной по отношению к матрице и обозначается A ^T:

,  .

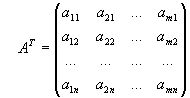Вернысоотношения: (A^T )^T =A; (A+B)^T=A^T +B^T ; (AB)^T =B^T A^T.

Квадратная матрица A, для которой A ^T =A, называется симметричной. Элементы такой матрицы, расположенные симметрично относительно главной диагонали, равны.

Квадратная матрица A называется обратимой, если существует такая матрица X, что AX=XA=E.  Матрица X называется обратной к матрице A и обозначается A ^-1, т.е.  A A ^-1 =A ^-1A=E.

Известно, что если матрица A невырождена (т.е ее определитель отличен от нуля), то у нее существует обратная матрица A ^-1.

Верно соотношение: (A^-1)^T =(A^T ) ^-1.

 

 

2.ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКОВ, ИХ ОСНОВНЫЕ СВОЙСТВА.   

Определение 1.4. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:

                      .

При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего вправый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.

 

Примеры.

 

1.            

 

Определение 1.5. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:

 

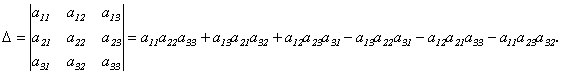
Можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:

 

 образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали: 

 

 

Примеры.

 

 

 

                            Основные свойства определителей.

 

 

Свойство 1. Определитель не изменяется при транспонировании, т.е.

                   

 

Доказательство.

 

 

=    

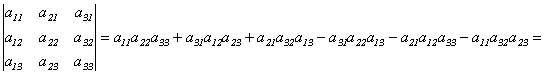
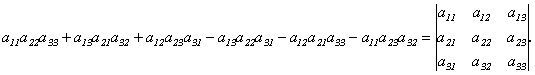
Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.

                             .

 

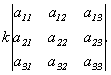Доказательство.

 

        

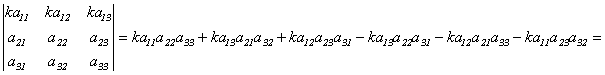
Свойство 3. Определитель, имеющий нулевую строку, равен 0.   

                               

 

Свойство 4. Определитель, имеющий две равные строки, равен 0.

                             

                            

Доказательство.

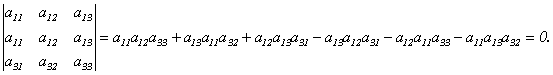
Свойство 5. Определитель, две строки которого пропорциональны, равен 0.

                           

Свойство 6. При перестановке двух строк определителя он умножается на –1.

                   

 

Доказательство.

 

 

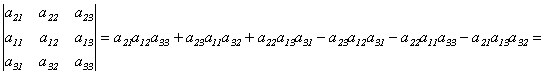
Свойство 7.

 

 

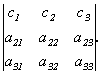
Свойство 8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.