Вопрос 1. Связь фпм и фпф объективов с децентрировкой и расфокусировкой.

Децентрировку можно уменьшить до допустимой величины, если линзу в оправе на специальном центрировочном патроне смещать и разворачивать таким образом, чтобы центры кривизны ее поверхностей совместились с осью вращения шпинделя токарного станка, после чего обработать базовые поверхности оправы. При этом оптическая ось линзы совмещается с геометрической осью оправы с требуемой точностью.

Рассмотрим схематически процесс центрирования линзы. На рисунке изображена линза, установленная в центрировочном патроне. Линза установлена так, чтобы центр кривизны наружной поверхности линзы О₁ был расположен в одной плоскости с центром кривизны О сферической части патрона. Центры кривизны поверхностей линзы O₁ и О₂ смещены относительно оси шпинделя станка и при вращении шпинделя описывают окружности. Смещения центров кривизны с оси вращения шпинделя наблюдают и измеряют с помощью автоколлимационной центрировочной трубки ЮС-13, разработанной А. А. Забелиным. Трубку укрепляют на задней бабке токарного станка. Вращением винтов 1, расположенных через 90° вокруг оси шпинделя, подвижную часть патрона смещают в плоскости, перпендикулярной к оси шпинделя, так, что центр кривизны линзы O₁ совмещается с осью шпинделя . Биения центра кривизны О₁ при вращении шпинделя в этом случае не наблюдается, биение центра кривизны О₂ увеличивается. Вращением винтов 2, перемещающих сферическую часть патрона, центр кривизны О₂ совмещают с осью шпинделя (рис. 1). При этом центр кривизны О₁ не смещается с оси шпинделя, так как он был расположен в одной плоскости с центром сферической части патрона. При вращении шпинделя биение обоих центров кривизны линзы отсутствует. В результате оправа линзы будет иметь перекос, но оптическая ось линзы будет совмещена с осью шпинделя. Вызванный юстировкой перекос оправы устраняют проточкой резцом 3 ее торца и наружной поверхности, не снимая-линзы с центрировочного патрона. Наружную поверхность оправы линзы с Ø 20** протачивают до размера, равного диаметру корпуса объектива, с минимально необходимым зазором (порядка 0,01 мм).

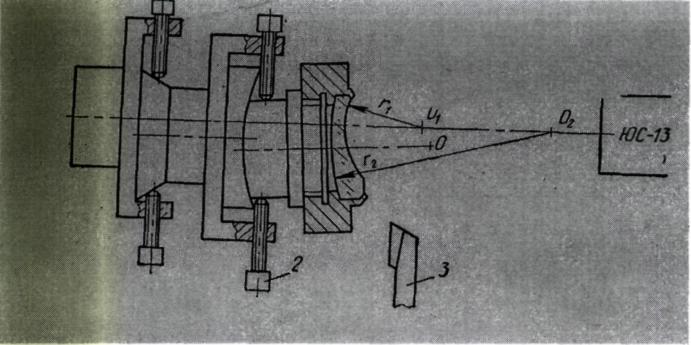
Рис. 1 Центрирование линзы.

Торец оправы подрезают так, чтобы можно было выдержать указанный на чертеже линзы размер 0,54 ± 0,01 мм (см. рис. 2).

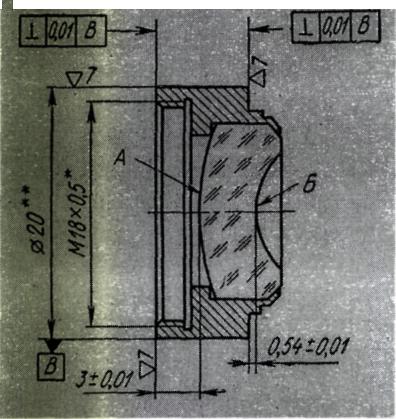
Рис. 2 Пример чертежа линзы для автоколлимационной сборки.

Расстояние от линзы до торца при подрезке измеряют индикаторным приспособлением. Затем линзу снимают с центрировочного патрона и устанавливают в цанговый патрон токарного станка на обработанные базовые поверхности. Подрезают второй опорный торец оправы таким образом, чтобы выдержать размер 3 ± 0,01 мм до второй поверхности линзы. Процесс центрирования линзы окончен.

Оптическая передаточная функция является наиболее полной характеристикой для оценки качества фотографических, проекционных, телевизионных и им подобных объективов. Перечисленные объективы, воспроизводящие оптическое изображение в основном для визуального восприятия, должны обеспечивать передачу крупных деталей с большей резкостью и с большим контрастом, чем очень мелких, близких к пределу разрешения. Это объясняется, прежде всего, тем, что при визуальном рассмотрении художественного снимка, телевизионного или проекционного изображения, уделяется меньше внимания распознаванию мелких деталей, чем крупных, и поэтому значительно большую роль играет качество передачи крупных структур предметов. В связи с этим знание того, с какой интенсивностью (амплитудой выходного синусоидального сигнала) и смещением по полю снимка (фазой) передает объектив ту или иную пространственную частоту, характеризующую размер предметов, представляет большой интерес в оценке качества изображения.

Математическое выражение оптической передаточной функции можно получить из уравнения, описывающего процесс образования оптического изображения в частотном представлении:

~E(N_xN_y) = ~A(N_xN_y) ~L(N_xN_y).

Из этого уравнения следует, что преобразование Фурье функции распределения освещенности в изображении отличается от преобразования Фурье функции распределения яркости в предмете коэффициентом ~A(N_xN_y), который и назван оптической передаточной функцией.

Коэффициент изменения амплитуды будет

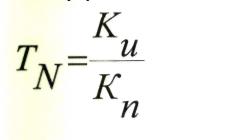
Это отношение называют коэффициентом передачи контраста данной пространственной частоты (или коэффициентом передачи модуляции — КПМ). Изменяя пространственную частоту N, получим зависимость изменения амплитуды от пространственной частоты, т.е. амплитудно-частотную характеристику и зависимость изменения фазы от пространственной частоты — частотнофазовую характеристику. Таким образом, амплитудно-частотная характеристика показывает зависимость коэффициента передачи модуляции от пространственной частоты и называется функцией передачи модуляции (ФПМ), или частотно-контрастной характеристикой и обозначается Т (N). Зависимость изменения фазы от пространственной частоты называется функцией передачи фазы (ФПФ), или частотно-фазовой характеристикой, и обозначается (p(N). Графическое представление этих характеристик для типового случая дано на

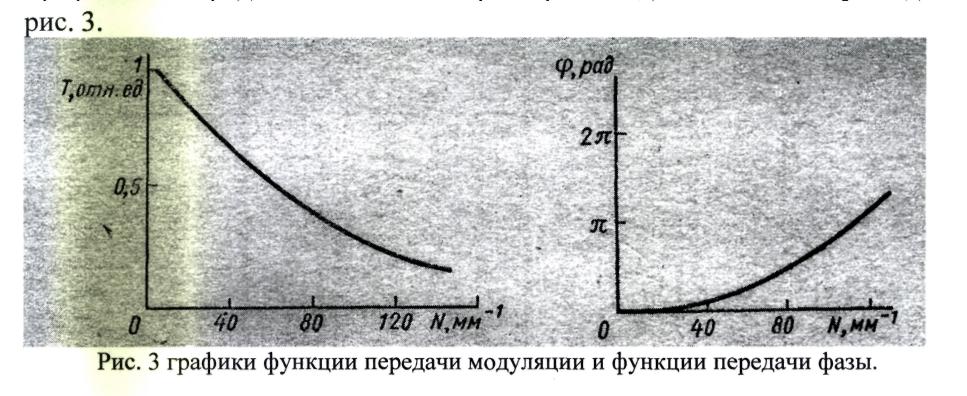
Для нулевой пространственной частоты ФПМ имеет максимальное значение и приводится к единице (нормируется), а ФПФ- равна нулю: