79.В 52 написано про н.С.О.

Во всех инерциальных системах отсчета ускорение тел одинаково, при переходе от одной инерциальной системы отсчета к другой справедливы закон сложения скоростей Галилея и преобразования координат Галилея

СЛОЖЕНИЯ СКОРОСТЕЙ ЗАКОН

- определяет связь между значениямискорости материальной точки по отношению к разл. системам отсчёта, движущимсядруг относительно друга. В нерелятивистской физике, когда рассматриваютсяскорости, малые по сравнению со скоростью света с, справедлив законсложения скоростей Галилея:

где u и u' - скорости частицы в двух инерциалъных системах отсчётаК т К' соответственно (система К' движется относительно . со скоростью v). Если скорости движения близки к е, то ф-ла(1) неприменима и справедлив С. с. з. частной (специальной)относительноститеории:

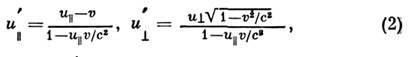
где и  - проекции скорости частицы в системе  отсчёта К(К' )на направления параллельное и перпендикулярное к v.В пределе  и   ф-лы(2) переходят в (1). В случае, когда скорости и и v параллельны,(2) переписывается в виде 

Из ф-лы (3), в частности, следует, что если и = с, то и и'= с независимо от в, т. е. абс. величина скорости света не зависитот движения системы отсчёта. Тот же вывод справедлив, разумеется, и припроизвольном направлении скоростей, когда надо пользоваться ф-лой (2).

В случае неравномерных относит. движений двух систем отсчёта, а такжепри наличии тяготения (т. е. в случае общей теории относительности)все приведённые соотношения справедливы в локально сопутствующих инерциальныхсистемах отсчёта  , т. е. в таких бесконечно малых системах отсчёта, к-рые в данный моменти в данном месте неподвижны относительно рассматриваемых систем К кК'соответствепно и в к-рых в этот момент нет сил ускорения и нет вращенияи деформаций, т. е. они локально инерциальны.

80. Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости .

При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например M₁M₂ ) совершают одинаковые движения.

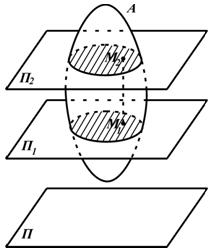Отрезок M₁M₂  движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости.

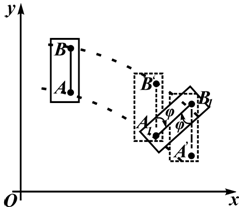На рисунке 2.12 показано перемещение пластинки в плоской системе отсчета xOy  из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A  с последующим поворотом на угол φ  вокруг точки A₁. Это же перемещение можно выполнить иначе. 

Например, перемещая пластинку поступательно с траекторией точки B , с последующим поворотом вокруг B₁  на угол φ. Траектории точек A  и B различны, а угол поворота в обоих случаях  одинаков. 

Положение пластинки вполне определяется положением скрепленного с ней отрезка (например AB), закон движения которого можно задать в виде:

x_A=x_A(t),  y_A=y_A(t),  φ=φ(t).

Точка A  в этом случае называется полюсом. Если принять за полюс точку B , то получим уравнения:

                                x_B=xB(t),  y_B=yB(t),  φ=φ(t)

За полюс выбирается точка, закон движения которой известен.

81.энергия покоя в 51, закономерность массы и энергии в 48

82. в 65 тоже самое

83. Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.

Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров и т.д.

Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.

Доказательство. 

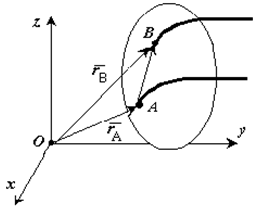
Если выбрать две точки твердого тела А  и В  ,то радиусы-векторы этих точек связаны соотношением

Траектория точки А  – это кривая, которая задается функцией r_A(t), а  траектория точкиB – это кривая, которая задается функцией r_B(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.

Продифференцируем по времени выражение

Получаем

Продифференцируем по времени скорость и получим выражение a_B = a_A. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.

Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

85. и.с.о. в 70

первого закона Ньютона (закона инерции): существуют такие системы отсчета, относительно которых тело (материальная точка) при отсутствии на нею внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.

Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными. Следовательно, инерциальными являются такие системы отсчета, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно.

88. Силы инерции — силы, обусловленные ускоренным движением неинерциальной системы отсчета (НСО) относительно инерциальной системы отсчета (ИСО). Основной закон динамики для неинерциальных систем отсчета:  , где   — сила, действующая на тело со стороны других тел;

  — сила инерции, действующая на тело относительно поступательно движущейся НСО. Где a0 — ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;

  — центробежная сила инерции, действующая на тело относительно вращающейся НСО.   — угловая скорость НСО относительно ИСО, R — расстояние от тела до центра вращения;

  — кориолисова сила инерции, действующая на тело, движущееся со скоростью V относительно вращающейся НСО.    — угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).

89.

Рассмотрим действие внешней силы  , приложенной к точке массой  . За время   элементарная масса   проходит путь   Работа силы   на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей   силы.

Но   равна модулю момента   силы   относительно оси вращения. Работа  , и будет положительна, если   имеет такое же направление, как и   отрицательное, если направление векторов   и   противоположны.

С учетом, что 

Работа всех сил, приложенных к телу

(5.13)

Полная работа

(5.14)

90. О́пыты Ма́йкельсона — класс физических экспериментов, исследующих зависимость скорости распространения света от направления. В настоящее время (2011 год) точность опытов позволяет найти относительные отклонения изотропности скорости света в единицы 10⁻¹⁶, однако на этом уровне отклонения не найдены. Опыты Майкельсона являются эмпирической основой принципа инвариантности скорости света, входящего в общую теорию относительности (ОТО) и специальную теорию относительности (СТО).

Вычисляем общее время t1 используя сумму времен двух путей:

Приближение связано с тем, что (V²/c²)<<1 (порядка 10^-8)  когда берется скорость V, что и у земли.

Скорость эфира c=IIV+V1II, а V1=IIV1II скорость волны в направлении зеркала.

из этого следует, что:

Принимая во внимание симметрию, мы можем теперь вычислить:

Разность фаз пропорциональна:

 где   пропорциональна разности фаз, при повороте на  :

Было показано, что теория эфира подразумевает разность, поддающуюся количественной оценке, и обнаруживаемую соответствующими средствами (интерферометр Michelson–Morley).