57. Основное уравнение релятивистской динамики

     В ньютоновой механике обычная трехмерная 3-сила определяется как скорость изменения во времени количества движения, переносимого на данное тело от окружающих тел и полей (равенство   Ньютона является одновременно и определением силы, и законом движения). Аналогично поступим и в релятивистской механике, не забывая в то же время, что делить (множить) следует только на инвариантные величины.

     По определению 4-сила  - это скорость изменения 4-импульса, оцененная в течение собственного времени движущегося тела (точки; частицы), т.е.  . Подставляя значение 4-импульса, можно представить 4-силу в виде

     

     или

       =

     Подставив значение   и учтя явный вид компонент импульса   и  , получим величину

     

(8.4)

     Так выглядит 4-сила в системе I (в которой время t, скорость  ). Ниже структура   будет представлена в более компактном виде.

     Здесь возникает важный вопрос: если при скоростях значительно меньших скорости света (), т.е. в ньютоновой механике, сила определяется по второму закону Ньютона равенством  (индекс "н" указывает на ньютонову механику), то как следует обобщить понятие 3-силы на любые скорости, вплоть до как угодно близких к скорости света?

     Ответ на такие вопросы может давать только практика, эксперименты, опыт. Вся современная экспериментальная физика подтверждает, что под релятивистской 3-силой следует понимать величину, являющуюся производной от релятивистского 3 импульс

     

(8.5)

     Это равенство обобщает ньютонову трактовку 3-силы. В то же время оно представляет основной закон движения частицы (материальной точки) в инерциальной системе отсчета при любыхвозможных скоростях меньших с.

     Рассмотрим закон преобразования компонент 4-силы, представленных формулой (8.4). Учитывая (8.5), представим 4-силу в окончательном виде

     

(8.6)

     Как видим, в структуру 4-силы Минковского   входит релятивистская

     трехмерная сила   и ее мощность  .

     Рассмотрим дальше преобразование компонент 4-силы при переходе от ИСО I к ИСО П, которая движется со скоростью v относительно системы I в направлении оси х. При этом в системе I предполагается известным мгновенное значение скорости точки  (v_x,v_y,v_z) и сила  . Преобразование 4-силы позволит определить также и величину трехмерной силы в системе II. Как уже указывалось, преобразование компонент 3-векторов определяется на основе сначала преобразования 4-векторов (при переходе  ). Итак, нужно подвергнуть компоненты 4-силы  , т.е.

     

(8.7)

     преобразованиям Лоренца. Применяя их к (8.7), получим четыре формулы, дающие окончательный вариант преобразований

     

(8.8a)

     

(8.8b)

     Следовательно, при переходе от системы отсчет I к системе II проекции 3-силы   изменяются; они остаются неизменными в нерелятивистском случае, когда  . Первая из полученных формул определяет мощность силы в системе II, остальные три - проекции силы.

58. Достаточно продифференцировать   в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости.

Приведем более элементарный, но и более общий вывод — для случая произвольного движения начала отсчета одной системы относительно другой (при отсутствии вращения). Для такого более общего случая, можно получить формулу преобразования скоростей, например, так.

Рассмотрим преобразование произвольного сдвига начала отсчета на вектор  ,

где радиус-вектор какого-то тела A в системе отсчета K обозначим за  , а в системе отсчета K' — за  ,

подразумевая, как всегда в классической механике, что время   в обеих системах отсчета одно и то же, а все радиус-векторы зависят от этого времени:  .

Тогда в любой момент времени

и в частности, учитывая

,

имеем:

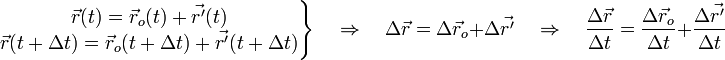
где:

 — средняя скорость тела A относительно системы K;

 — средняя скорость тела А относительно системы K' ;

 — средняя скорость системы K' относительно системы K.

Если   то средние скорости совпадают с мгновенными:

или короче

— как для средних, так и для мгновенных скоростей (формула сложения скоростей).

Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета. Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга:

59. Теорема об изменении кинетической энергии материальной точки.

Для доказательства теоремы запишем дифференциальное уравнение движения точки в виде mdV / dt = F. Умножая обе части уравнения скалярно на вектор элементарного действительного перемещения точки dr и учитывая, что dr / dt = V, имеем

(1)

Зная, что F - равнодействующая сил, приложенных к точке, обозначим δA скалярное произведение в правой части и назовем его элементарной работой сил, приложенных к точке:

(2)

Находя дифференциал от mV² / 2, имеем

Подставляя последнее выражение и выражение (2) в уравнение (1), получаем математическую запись теоремы в дифференциальной форме:

(3)

Половину произведения массы точки на квадрат ее скорости под знаком дифференциала в левой части уравнения (3) называют кинетической энергией точки.

Это замечание позволяет по математической записи сформулировать теорему об изменении кинетической энергии материальной точки в дифференциальной форме: дифференциал от кинетической энергии материальной точки равен элементарной работе сил, приложенных к точке.

Отметим, что кинетическая энергия - это еще одна, но уже скалярная, мера движения материальной точки, что дает ей определенные преимущества перед векторными мерами движения - количеством движения и моментом количества движения. В системе СИ единицей измерения кинетической энергии является джоуль, 1 Дж = кг·(м²/с²) = (кг·м/c²)·м = 1 Н·м.

Предположим, что при переходе точки из начального положения M₀ в конечное (или текущее) положение M ее скорость изменилась от начального значения V₀ до текущего (или конечного) значения V, и при этих предположениях проинтегрируем выражение (3). Тогда

Интеграл в правой части этого выражения обозначим A и назовем полной работой или просто работой сил, приложенных к материальной точке:

(4)

Учитывая введенное обозначение, получаем математическую запись теоремы об изменении кинетической энергии материальной точки в интегральной форме:

mV2 / 2 - mV02 / 2 = A

(5)

то есть: изменение кинетической энергии материальной точки при ее переходе из начального положения в текущее (или конечное) положение равна работе сил, приложенных к точке, совершенной при этом переходе.