
- •Замедление времени и инвариантность скорости света
- •46. Основное уравнение динамики относительного движения материальной точки.
- •Моменты инерции и тензор инерции.
- •Относительность движения
- •Кинематические характеристики[править | править исходный текст]
- •57. Основное уравнение релятивистской динамики
- •60. Следствия из преобразований Лоренца
- •61. Закон изменения и сохранения полной механической энергии
- •62. Кинетическая энергия вращающегося твердого тела
- •69. В 48 тоже самое
- •79.В 52 написано про н.С.О.
Относительность движения
Как следует из определения механического движения, оно представляет собой изменение положения тела относительно других тел. Следовательно, понятие относительности движения входит уже в само определение понятия механического движения. Сущностьотносительности движения заключается в том, что описать какое-либо движение можно только сделав выбор тела, относительно которого данное движение будет рассмативаться, т. е. выбрав тело отсчета.
Как было отмечено, совокупность тела отсчета, связанной с ним системы координат и часов образует систему отсчета. Движение одного и того же тела описывается по-разному относительно различных систем отсчета. Особенно сильно отличаются описания движения тел относительно разных систем отсчета в том случае, когда эти системы сами движутся друг относительно друга.
55. Враща́тельное движе́ние — вид механического движения. При вращательном движении материальной точки она описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Осьвращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения роторагенератора на электростанции неподвижна.
Кинематические характеристики[править | править исходный текст]
Вращение
характеризуется углом ![]() ,
измеряющимся в градусах или радианах, угловой
скоростью
,
измеряющимся в градусах или радианах, угловой
скоростью ![]() (измеряется
в рад/с) и угловым
ускорением
(измеряется
в рад/с) и угловым
ускорением ![]() (единица
измерения — рад/с²).
(единица
измерения — рад/с²).
При равномерном вращении (T - период вращения),
Частота вращения — число оборотов в единицу времени.
![]() ,
,
Период вращения — время одного полного оборота. Период вращения
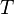 и
его частота
и
его частота 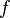 связаны
соотношением
связаны
соотношением 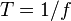 .
.
Линейная скорость точки, находящейся на расстоянии R от оси вращения
![]() ,
,
Угловая скорость вращения тела
![]() .
.
56.
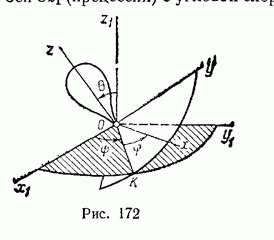

Уравнение Эйлера:
В системе отсчёта стороннего наблюдателя уравнения вращательного движения имеют вид
![]()
В
таком виде уравнения мало применимы
для практики, поскольку, в общем случае,
оба компонента момента импульса —
тензор момента инерции и псевдовектор
угловой скорости — зависят от времени.
Идея Эйлера состояла в том, чтобы перейти
в систему отсчёта, жёстко связанную с
вращающимся телом. В этой системе тензор
момента инерции постоянен, и его можно
вынести за производную. Для дальнейшего
упрощения мы выбираем в качестве
фиксированных осей тела его главные
оси инерции. Таким образом мы можем
разделить изменение углового
момента на
компонент, который описывает изменение
величины ![]() и
компонент, который компенсирует это
изменение в направлении
.
и
компонент, который компенсирует это
изменение в направлении
.
Тогда уравнения принимают вид:
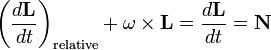
где
— угловой
момент тела
по отношению к пространственным осям, 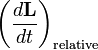 —
изменение углового
момента тела
по отношению к его фиксированным
осям,
—
изменение углового
момента тела
по отношению к его фиксированным
осям, ![]() скорость
изменения углов
Эйлера осей,
связанных с телом, по отношению к
пространственным осям, и
скорость
изменения углов
Эйлера осей,
связанных с телом, по отношению к
пространственным осям, и ![]() —
внешний вращающий момент.
—
внешний вращающий момент.
если
мы заменим
его
компонентами ![]() ,
то мы можем заменить
,
то мы можем заменить ![]() выражением
выражением ![]() .
если мы выберем базовые вектора
.
если мы выберем базовые вектора ![]() совпадающими
с главными осями инерции тела, то первые
три слагаемых равны
,
а остальные три — это
совпадающими
с главными осями инерции тела, то первые
три слагаемых равны
,
а остальные три — это ![]() .
.
Тогда уравнения Эйлера в компонентной форме примут вид:

Также возможно использовать эти три уравнения, если оси, в которых записан не связаны с телом. Тогда должен быть заменён вращением осей вместо вращения тела. Тем не менее, все ещё требуется, чтобы выбранные оси были главными осями инерции! Эту форму уравнений Эйлера удобно использовать для объектов, обладающих вращательной симметрией, что позволяет произвольно выбирать некоторые из главных осей инерции.
