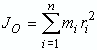Моменты инерции и тензор инерции.

Понятие момента инерции принадлежит к числу основных и важных понятий в динамике.

Различают следующие моменты инерции: осевые J_x, J_y, J_z; полярный J_O; центробежные J_xy = J_yx, J_xz = J_zx, J_yz = J_zy. Моменты инерции определяются в системе координат Oxyz. Они могут быть вычислены для отдельной материальной точки, системы материальных точек и твердого тела.

Осевой момент инерции, как будет показано, является физической величиной, характеризующей инерционность твердого тела во вращательном движении вокруг неподвижной оси. При вращении твердого тела вокруг неподвижной точки его инерционность характеризует момент инерции относительно мгновенной оси, проходящей через неподвижную точку.

Осевой момент материальной точки равен произведению массы точки на квадрат расстояния до соответствующей оси (рис. 18):

(7)

Полярный момент инерции материальной точки равен произведению массы точки на квадрат расстояния до начала координат:

JO = mr2 = m(x2 + y2 + z2)

(8)

Из выражений (7) и (8) следует, что сумма осевых моментов инерции равна удвоенному полярному моменту инерции:

Jx + Jy + Jz = 2JO

(9)

В этом нетрудно убедиться, сложив осевые моменты в (7), учитывая выражение (8).

Центробежный момент материальной точки равен произведению массы точки на произведение двух ее координат:

Jxy = Jyx = mxy; Jxz = Jzx = mxz; Jyz = Jzy = myz

(10)

Осевыми, центробежными и полярным моментами инерции системы являются суммы соответствующих моментов инерции всех материальных точек системы. Если система состоит из n материальных точек, то

	(11)
	(12)
	(13)

Для твердого тела дискретные суммы в последних выражениях можно выразить интегралами по массе тела:

	(14)
	(15)
	(16)

Отметим, что соотношение между осевыми и полярным моментами инерции (9) выполняется и в системе материальных точек и в твердом теле.

Момент инерции твердого тела относительно оси (осевой момент инерции), например оси Oz, можно представить в виде произведения массы всего тела на квадрат линейной величины, называемой радиусом инерции:

Jz = Mρz2

(17)

Радиус инерции ρ_z определяет расстояние от оси Oz до материальной точки, в которой сосредоточена масса всего тела, так чтобы момент инерции полученной точки относительно оси Ozравнялся моменту инерции тела относительно той же оси. Из формул (6) - (16) следует, что моменты инерции измеряются в кг·м².

Момент инерции относительно произвольной оси Ou, проходящей через данную точку (начало координат), вычисляется по формуле

(18)

где μ, λ, ν - направляющие косинусы оси Ou в системе координат Oxyz (рис. 19), равные λ = cosα; μ = cosβ; ν = cosγ.

Тензором инерции в данной точке (начале координат) называется матрица, составленная из осевых и центробежных моментов инерции, вида

(19)

которая характеризует распределение масс в системе и твердом теле относительно системы координат с началом в данной точке. Иногда в обозначении тензора инерции применяют надстрочные и подстрочные индексы, например θ_A^(x1y1z1) или θ_A⁽¹⁾, что означает тензор инерции для точки A, который вычислен в системе координат Ax₁y₁z₁.

Тензор инерции определяет инерционные свойства и распределение масс системы материальных точек и твердого тела в данное мгновение времени, так как r_i, x_i, y_i, z_i меняются с течением времени. Однако в связанной с твердым телом системе координат (рис. 21) они остаются постоянными, то есть постоянными будут и моменты инерции, что дает значительные преимущества при решении задач динамики. Поэтому моменты инерции и тензор инерции твердого тела нужно вычислять в связанной с ним системе координат.

Из изложенного выше следует, что девять величин полностью характеризуют распределение масс системы материальных точек (твердого тела). Это три статических момента инерции, определяющие положение центра масс в системе координат; три осевых и три центробежных момента инерции, составляющие тензор инерции.

52.Есть в тетради

относительное движение — это движение материальной точки/тела относительно подвижной системы отсчёта.