25. Уравнение механических волн. Ударные волны.

Механической волной называют механические возмущения, распространяющиеся в пространстве и несущиеся энергию.

Различают два основных вида механических волн: упругие волны – распространение упругих деформаций – и волны на поверхности жидкости.

Упругие волны возникают благодаря связям, существующим между частицами среды: перемещение одной частицы от положения равновесия приводит к перемещению соседних частиц. Этот процесс распространяется в пространстве с конечной скоростью.

Уравнение волны выражает зависимость смешения колеблющейся точки, участвующей в волновом процессе, от координаты ее равновесного положения и времени. Для волны, распространяющейся вдоль направления ОХ, эта зависимость записывается в общем виде:

Если s и х направлены вдоль одной прямой, то волна продольная, если они взаимно перпендикулярны, то волна поперечная.

s= A cos w t s = A cos w (t-^x/_v) _x

_{o x}

Выведем уравнение плоской волны.

Пусть волна распространяется вдоль оси ОХ без затухания. Задания колебании точки с координатой х = о ур-ем

(1).

До точки с некоторой произвольной координатой х возмущение от начала координат дойдет через время τ, поэтому колебания этой точки запаздывают:

(2).

Т.к время и скорость распространения волны связаны зависимость

то вместо (2). получим

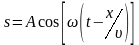(3).

Уравнение плоской волны, которое позволяет определить смещение любой точки. Аргумент при cos называют фазой волны. Множество точек, имеющих одновременно фазу называют фронтом волны.

Длиной волны называют расстояние между двумя точками, фазы которых в один и тот же момент времени отличаются на 2П. Она равна расстоянию, пройденному волной за период колебания

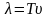(4).

Ударные волны

Один из распространенных примеров механической волны – звуковая волна. В этом случае максимальная скорость колебаний отдельной молекулы воздуха составляет несколько см в секунду даже для достаточно большой интенсивности.

Однако при больших возмущениях (взрыв, сверхзвуковое движение тел, мощный электрический разряд) скорость колеблющихся частиц среды может уже сравнимой со скоростью звука, возникает ударная волна.

При взрыве высоко-нагретые продукты, обладающие большой плотностью, расширяются и сжимают слои окружающего воздуха. С течением времени объем сжатого воздуха возрастает. Поверхность, которая отделяет сжатый воздух от невозмущенного, в физике называют ударной волной.

Ударная волна может обладать значительной энергией, так при ядерном взрыве на образование ударной волны в окружающей среде затрачивается около 50% энергии взрыва. Поэтому ударная волна, достигая биологических и технических объектов, способна причинить смерть, увечья и разрушения.