Затухающие колебания.
При изучении гармонических колебаний не учитывались силы трения и сопротивления, которые существуют в реальных системах. Действие этих сил существенно изменяют характер движения, колебание становится затухающим.
Если в системе
кроме квазиупругой силы действуют силы
сопротивления среди (силы трения), то
второй закон Ньютона можно записать
так:
(17).
Для решения
этого дифференциального уравнения
необходимо знать, от каких параметров
зависит сила трения. Обычно предполагают,
что при не очень больших амплитудах и
частотах сила трения пропорциональна
скорости движения и, естественно,
направлена противоположно ей:
(18).
r – коэффициент трения. Подставим (18) в (17)
или (19).
коэф. затухания, wо – круговая частота.
При круговая частота w является действительной величиной к решение будет следующим:
(20).
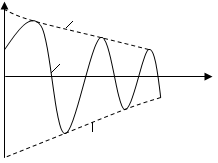
(Уравнение затухающих колебаний)
График этой функции показан на рисунке сплошной кривой
х
Ао 2
1
0 t
2
Период затухающих колебаний зависит от коэффициентов трения и определяется
Формулой
(21).
Быстрота
убывания амплитуды колебаний определяется
коэффициентом
затухания: чем
больше
,
тем сильнее тормозящее действие среды
и тем быстрее уменьшается амплитуда.
На практике, степень затухания часто характеризуют логарифмическим декрементом затухания, понимая под этим величину, равную натуральному логарифму. Отношения двух последовательных амплитуд колебаний, разделенных интервалом времени, равны периоду
(22).
Незатухающие и затухающие колебания называют собственными или свободными. Они возникают вследствие начального смещения или начальной скорости и совершаются при отсутствии внешнего воздействия за счет первоначально накопленной энергии.
Вынужденные колебания
Вынужденными колебаниями называются колебания, возникающие в системе при участии внешней силы, изменяющейся по периодическому закону.
Предположим, что на мат. точку кроме квазиупругой силы и силы трения действует внешняя вынужденная сила
Fo – амплитуда, w – круговая частота. Составим диф. уравнение
(23).
(24).
