22. Сложение гармонических колебаний. Сложное колебание. Гармонический спектр

сложного колебания.

Сложение гармонических колебаний.

Материальная точка может одновременно участвовать в нескольких колебаниях. В этом случае, чтобы найти уравнение и траекторию результирующего движения, следует сложить колебание.

Рассмотрим 2 такие задачи.

а). Сложение гармонических колебаний, направленных по одной прямой.

Пусть материальная точка одновременно участвует в двух колебаниях, происходящих вдоль одной линии. Аналитические такие колебания выражаются следующими уравнениями.

(12).

Частоты складываемых колебаний одинаковы тогда результирующее смещение точки

(13).

б) Сложение взаимно перпендикулярных гармонических колебаний.

Пусть материальная точка одновременно участвует в двух колебаниях: одно направлено вдоль оси ОХ, другое – вдоль оси ОУ. Колебания заданы следующими уравнениями:

(14).

Д опустим, что частоты складываемых колебаний одинаковы

тогда результирующее смещение точки

(15).

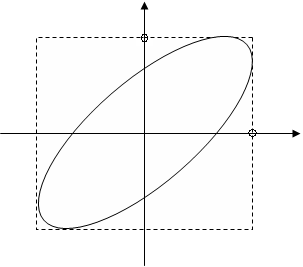
Уравнение (15) задают траекторию движения материальной точки в параметрической форме. Если в эти уравнения подставлять разные значения t, то можно определить координаты х и у, а совокупность координат и есть траектория. Траекторию можно представить в виде зависимости y =f (х), для получения которой следует исключить время из уравнений. Произведя математические преобразования, получим уравнение эллипса

у (16).

у=А₂

х

о. х=А₁

При одновременном участии двух взаимно перпендикулярных гармонических колебаниях одинаковой частоты материальная точка движения по эллиптической траектории. При сложении взаимно перпендикулярных колебаний разных частот получаются различные траектории материальной точки, названные фигурами Лиссажу.

Сложное колебание гармонический спектр сложного колебания.

Сложение колебаний приводит к более сложным формам колебаний.

Для практических целей бывает необходимой противоположная операция: разложение сложного колебания на простые, обычно гармонические.

Фурье показал, что периодическая функция любой сложности может быть представлена в виде суммы гармонических функций, частоты

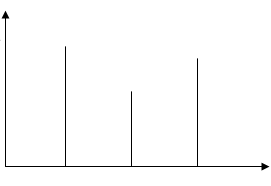
которых кратны частоте сложной периодической функции. Такое разложение периодической функции на гармонические и , следовательно, разложение различных периодических процессов на гармонические колебания называется гармоническим анализам. Автоматически гармонический анализ колебаний, в том числе и для целей медицины, осуществляется специальными приборами - анализаторами. Совокупность гармонических колебаний, на которые разложено сложное колебание, называется гармоническим спектром сложного колебания . Гармонический спектр удобно представить как набор частот отдельных гармоник совместно с соответствующими им амплитудами. Гармонический анализ позволяет достаточно детально описать и проанализировать любой сложный колебательный процесс, он находит применение в акустике,

радиотехнике, электронике.

х

¹ ₄

³ ₂

t а) графики сложного колебания

А

б) гармонический спектр

О V1 V2 V3 V

23. Затухающие колебания. Вынужденные колебания.