20. Гармонические колебания. Уравнение гармонического колебания.

Повторяющиеся движения или изменения состояния называют колебаниями. Колебания распространяются в среде в виде волн. Среди различных видов колебаний наиболее простой формой являются гармоническое колебание, т.е такое, при котором колеблющаяся величина, изменяется в зависимости от времени по закону синуса или косинуса.

Например, материальная точка массой m подвешена на пружине. В этом положении упругая сила F, уравновешивает силу тяжести. Если

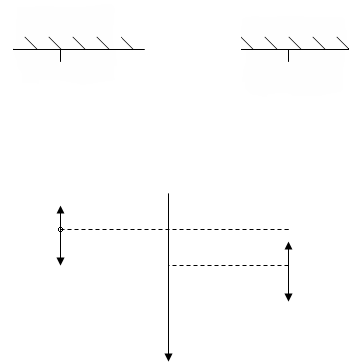
оттянуть пружину на расстоянии х, то на материальную точку будет действовать большая упругая сила. Изменение упругой силы, согласно закону Гука, пропорционально изменению длины пружины или смещению х точки:

F = -kx. (1).

«-» показывает, что сила всегда направлена в сторону положения равновесия.

Другой пример. Математический маятник отклонен от положения равновесия на небольшой угол α.

Т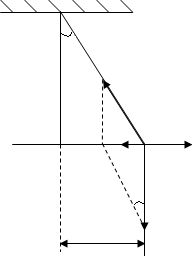 огда траекторию движения маятника можно считать прямой линией, совпадающей с осью ОХ. В этом случае выполняется приближенное равенство

α ≈ sin α ≈ tqα ≈ x/ℓ.

Х – смещение материальной точки

ℓ – длина нити маятника.

На материальную точку действует натяжения нити F_n и сила тяжести mg. Их равнодействующая работа

F=mgtgα = - mg ^х/e = k/_x (2).

k = ^mg/e (3).

Сравнивая (2) и (1) видим, что в этом примере равнодействующая сила подобна упругой, т.е пропорциональна смещение материальной точки и направлена к положению равновесия. Такие силы, неупругие по природе, но аналогичные по свойствам силам, возникающих при малых деформациях упругих тел, называют квазиупругими.

5.2 уравнение гармонического колебания

(4).

w_оt + φ_о = φ-фаза колебаний, φ_{о –} начальная фаза, w_о – круговая частота колебаний, А – амплитуда.

Период колебаний может быть найден из формулы

Т = ^2П/w_о (5).

Период пружинного маятника

(6).

Период математического маятника

(7).

21. Скорость и ускорение при колебательном движении.

Если в качестве колебательной системы использовать, например, математический маятник (рис. 6.3), то в процессе его движения происходит периодическое изменение скорости  и ускорения.

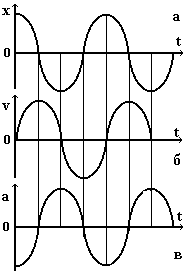
Рис. 6.3

При движении маятника после прохождения им положения равновесия в направлении к состоянию I (в ту же сторону направлен и вектор скорости маятника) скорость убывает, а ускорение  растет и в крайнем I состоянии скорость обращается в нуль, ускорение в этот момент времени достигает своего максимума и направлено по касательной к дуге окружности к положению равновесия.

 При обратном движении маятника к положению равновесия вектор скорости направлен в сторону движения. Модуль скорости растет по величине, в то время как ускорение убывает (направление вектора ускорения теперь совпадает с направлением движения  маятника).

При достижения положения равновесия в точке 0 скорость достигает максимума, а ускорение обращается в нуль. После прохождения этого состояния скорость начинает убывать, а ускорение увеличивается (теперь вектор ускорения направлен к состоянию покоя со стороны состояния II и противоположен вектору скорости). При достижении крайнего положения II скорость обращается в нуль, ускорение  достигает максимума.

При движении маятника из состояния II снова к положению равновесия скорость изменив направление  растет, соответственно ускорение, сохраняя направление прежним, убывает. В т. 0 скорость маятника максимальна, ускорение обращается в нуль. При дальнейшем движении маятника весь процесс периодически повторяется.

Найдем уравнения изменения  скорости и ускорения маятника при гармонических колебаниях. Дифференцируя уравнение смещения (6.1) по времени t, найдем уравнение изменения скорости в любой момент времени (первая производная):

(6.2)

или

v=ωA cos(ωt+φ₀+π/2)

где (А) - амплитудное значение скорости м.т., совершающей гармонические колебания.

Скорость опережает смещение по фазе на π/2 ( или  отстает - на 3π/2).

Вывод:  Скорость м.т. при колебательных процессах изменяется по гармоническому закону и является функцией времени.

Найдем уравнение изменения ускорения  как первую производную скорости по времени (вторая производная  смещения по времени):

.

(6.3)

или a=ω²Acos(ωt+φ_o+π).

Используя уравнение (6.1) получим:

а =  2х .

(6.4)

Вывод: Ускорение изменяется по гармоническому закону, является функцией времени и опережает колебания смещения по фазе на  и опережает колебание скорости по фазе на /2.

Величина  ²А является амплитудным значением ускорения.