Тема 2.4. Прямая на плоскости
Различные виды уравнений прямой на плоскости:
1) общее уравнение прямой:
;
(2.21)
2)
уравнение прямой по точке
и угловому коэффициенту
,
где
(
– угол наклона прямой к положительному
направлению оси
):
;
(2.22)
3) уравнение прямой с угловым коэффициентом:
;
(2.23)
4) параметрическое уравнение прямой:
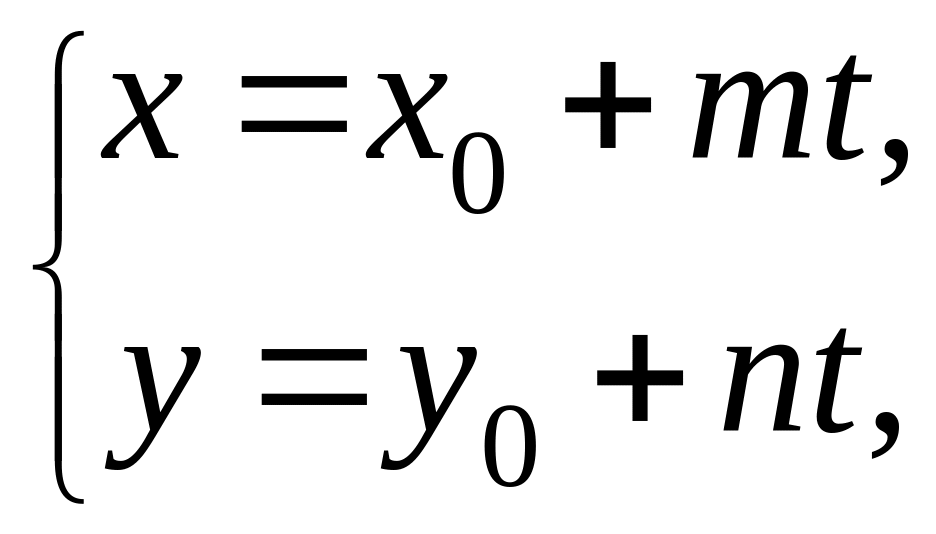(2.24)
где
– направляющий вектор прямой,
– точка, лежащая на прямой;
5) каноническое уравнение прямой:
;
(2.25)
6) уравнение прямой в «отрезках по осям»:
;
(2.26)
7) уравнение прямой, проходящей через две точки:
;
(2.27)
Тангенс
угла между прямыми
и
определяется по формуле:
.
(2.28)
Условие
перпендикулярности двух прямых:
.
Условие
параллельности двух прямых:
.
Расстояние
от точки
до прямой
вычисляется по формуле:
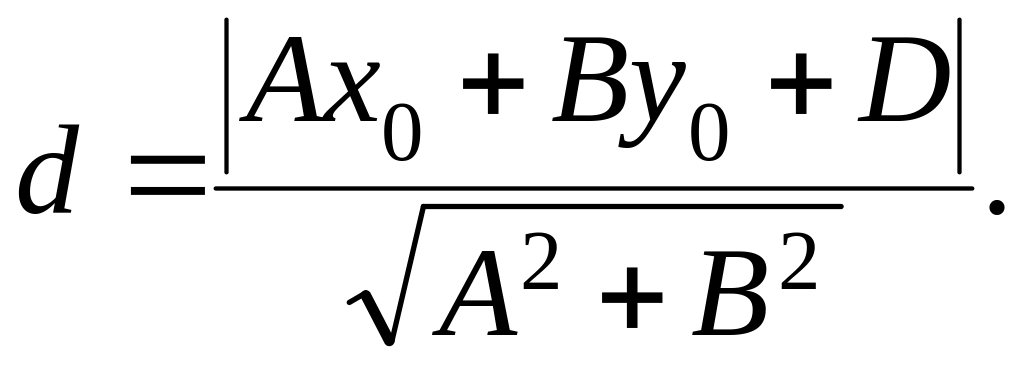(2.29)
Пример
2.19. Для прямой
записать ее уравнение в «отрезках по
осям».
Решение.
Преобразуем исходное уравнение прямой:
.
Для этого правую и левую части равенства
разделим на
:
.
Получили уравнение прямой, которое
соответствует уравнению (2.26).
Пример
2.20. Составить уравнение прямой,
проходящей через точки
и
.
Решение.
По формуле (2.27) имеем:
,
откуда
.
Окончательно получим
.
Пример
2.21. Доказать, что прямые
и
взаимно перпендикулярны.
Решение.
Приведем уравнения исходных прямых к
виду (2.23):
и
.
Запишем угловые коэффициенты:
и
.
Так как
,
то данные прямые перпендикулярны.
Раздел 3. Дифференциальное исчисление функции одной переменной
Тема 3.1. Пределы
Если
каждому натуральному числу n
по определенному закону ставится в
соответсятвие действительное число
,
то говорят, что задана числовая
последовательность
.
Например,
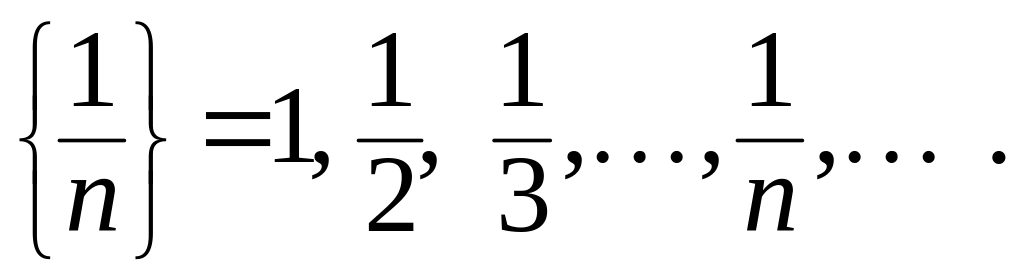
Число
называется пределом
последовательности
,
если для любого сколь угодно малого
числа
найдется номер N
(зависящий от
),
такой, что для всех членов последовательности
с номерами
выполняется неравенство
При этом пишут
.
Последовательность, имеющую предел,
называют сходящейся,
в противном случае – расходящейся.
Последовательность, предел которой
равен нулю, называют бесконечно
малой, а
последовательность, предел которой
равен бесконечности, – бесконечно
большой.
Например,
– бесконечно малая последовательность,
т.к.
,
а последовательность
является бесконечно большой, т.к.
Для
сходящихся последовательностей
и
,
таких, что
и
,
имеют место следующие теоремы о пределах:
|
|
|
|
.
.
.
.
Число
b
называется пределом
функции
в точке а,
если для любой последовательности
значений аргумента, сходящейся к числу
а,
соответствующая последовательность
значений функции
сходится к числу b
и записывают:
.
Из определения предела функции следует, что все теоремы о пределах последовательностей можно обобщить на случай предела функций.
Первым замечательным пределом называют предел вида
.
(3.1)
Следствия первого замечательного предела:
|
|
|
|
|
|
.
(3.2)
.
(3.5)
.
(3.3)
.
(3.6)
.
(3.4)
.
(3.7)
Вторым замечательным пределом называют предел вида
.
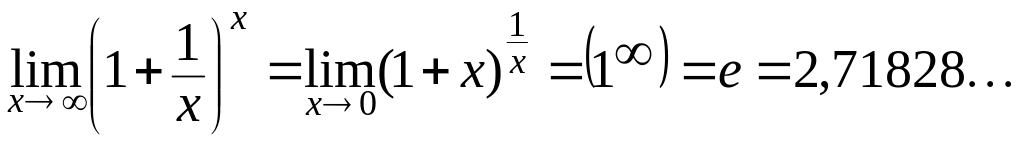(3.8)
Следствия второго замечательного предела:
|
|
|
|
|
|
.
(3.9)
.
(3.12)
.
(3.10)
.
(3.13)
.
(3.11)
.
(3.14)
Функция
называется бесконечно
малой при
,
если
Если отношение двух бесконечно малых
и
стремится к единице при
,
то
и
называются эквивалентными
бесконечно малыми
при
,
что обозначается так:
при
.
На
основании приведенных определений, а
также первого и второго замечательных
пределов и их следствий, можно записать
следующие соотношения эквивалентности
при
:
|
|
|
|
|
|
|
|
|
|
|
|
.
(3.15)
.
(3.20)
.
(3.16)
.
(3.21)
.
(3.17)
.
(3.22)
.
(3.18)
.
(3.23)
.
(3.19)
.
(3.24)
.
(3.25)