Метод Крамера
Метод Крамера также можно применять только для систем, у которых число уравнений равно числу неизвестных и определитель матрицы коэффициентов отличен от нуля. Решение такой системы находится по формулам Крамера:
(1.10)
где
– определитель матрицы
,
– определитель, полученный из
заменой его i-го
столбца столбцом свободных членов.
Метод Гаусса
Метод Гаусса заключается в последовательном исключении неизвестных и состоит из двух этапов: прямой ход – посредством эквивалентных преобразований система приводится к треугольному виду; обратный ход – решается полученная треугольная система, начиная с последнего уравнения. Эквивалентными преобразованиями системы являются:
– умножение любого уравнения системы на произвольное отличное от нуля число;
– замена местами строк системы;
– прибавление к какому-либо уравнению системы любого другого уравнения системы, умноженного на некоторое число.
Пример 1.6. Решить систему уравнений методом обратной матрицы, с помощью формул Крамера и методом Гаусса:
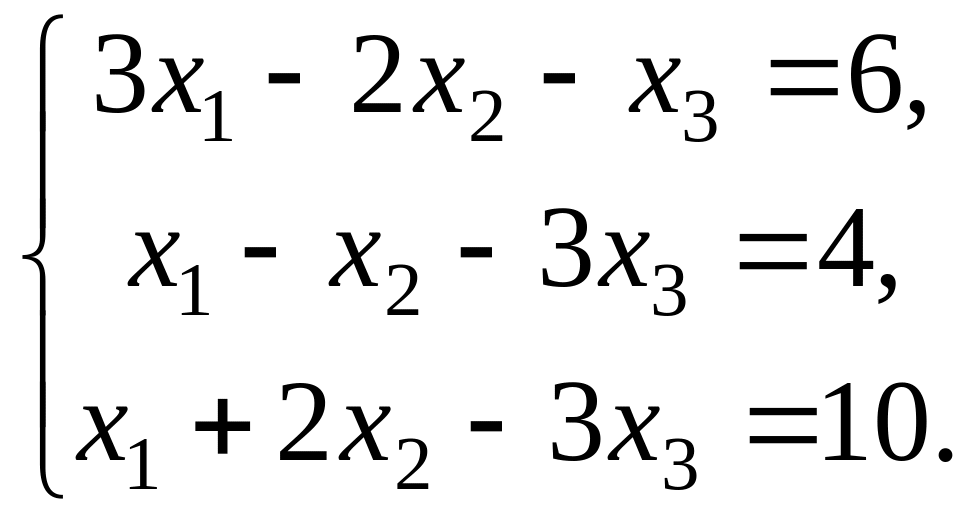
Решение. 1) Матричный метод. Запишем систему в матричном виде , где
;
;
.
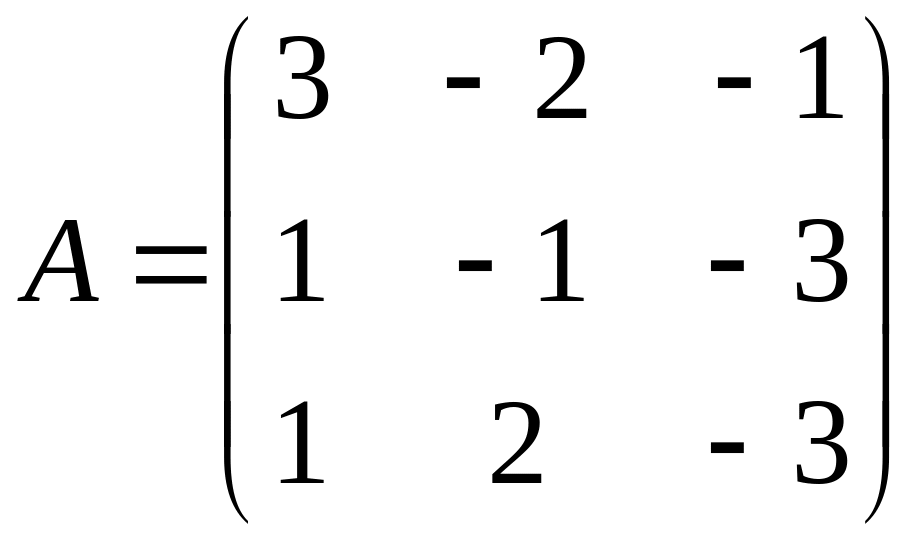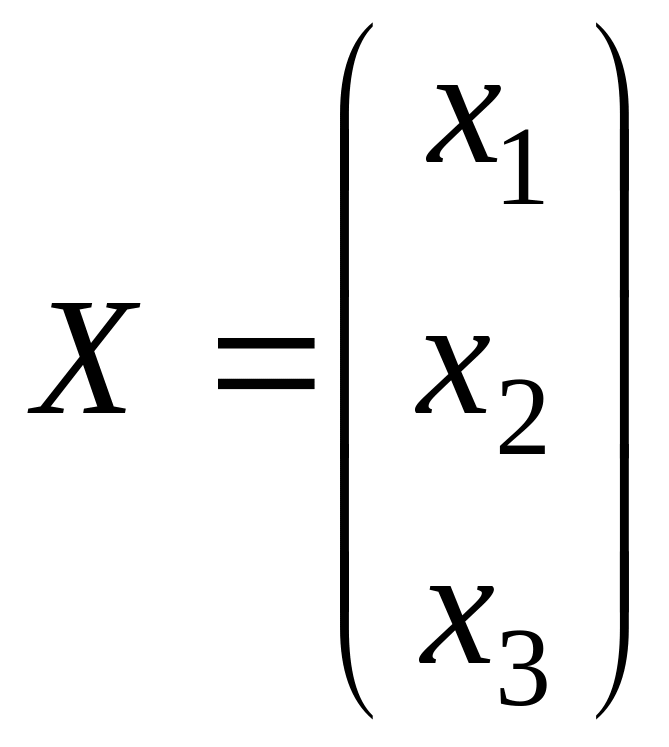Вычислим
.
Т.к. он отличен от нуля, то существует
обратная матрица
,
которую найдем по формуле (1.6):
Пользуясь
формулой (1.9), получим решение системы:
,
откуда
.
2)
Метод Крамера.
Выше было показано, что
.
Найдем
по формуле (1.3):
.
Далее по формулам (1.10) получим:
3) Метод Гаусса.
Прямой
ход.
Приведем расширенную матрицу системы
к треугольному виду:
.
Обратный ход. Запишем систему по приведенной матрице:
решая
которую, получим
.
Окончательно имеем: .
Пример 1.7. Найти решение системы уравнений методом Гаусса:
Решение. Осуществим эквивалентные преобразования строк расширенной матрицы системы, чтобы привести её к треугольному виду:
.
Получили
уравнение
,
значит, система несовместна.
Раздел 2. Элементы векторной алгебры и аналитической геометрии
Тема 2.1. Векторы
Вектором
называется направленный отрезок и
обозначается
или
.
Вектор характеризуется направлением
и модулем (длиной) или координатами.
Пусть
в ортонормированном базисе
начало вектора находится в точке
,
а конец в точке
.
Тогда координаты вектора
определяются по формуле:
.
(2.1)
Модуль вектора в базисе вычисляется по формуле
.
(2.2)
Над
векторами
и
можно совершать следующие линейные
операции:
– сложение
(вычитание):
;
– умножение
вектора на число:
,
где
– некоторое число.
Скалярным
произведением двух векторов
и
называется число, обозначаемое символом
,
и удовлетворяющее условиям:
1)
2)
;
3)
4)
Линейное пространство, в котором введено скалярное произведение, называют Евклидовым.
Длиной
или нормой любого вектора
называют арифметическое значение корня
квадратного из скалярного квадрата
:
.
Угол
между векторами определяется как угол,
изменяющийся в пределах от 0 до
радиан (от
до
).
Косинус угла между векторами
и
вычисляется по формуле
(2.3)
откуда
следует:
.
Векторы
и
называются ортогональными, если
угол между ними равен
.
Условие ортогональности векторов
и
:
если их скалярное произведение равно
нулю:
Векторы
образуют ортонормированный базис
линейного пространства, если эти векторы
взаимно ортогональны и их длины равны
единице:
Пусть векторы образуют ортонормированный базис линейного пространства. Тогда координаты векторов и в этом ортонормированном базисе записывают в виде
,
а их скалярное произведение и длины векторов принимают наиболее простую форму:
,
(2.4)
Косинус
угла между векторами
и
в произвольном ортонормированном базисе
вычисляется по формуле
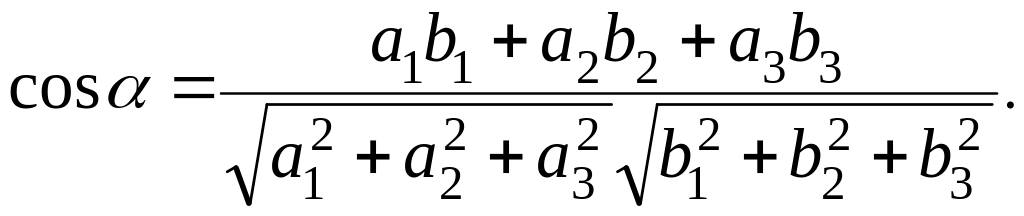(2.5)
Упорядоченная
тройка векторов
,
,
с общим началом в точке
называется правой, если кратчайший
поворот от вектора
к вектору
наблюдается с конца вектора
происходящим против хода часовой стрелки
(рис.2.1).
|
Рис.2.1 |
Векторным
произведением векторов
и
называется вектор
,
обозначаемый как
,
который удовлетворяет следующим трем
условиям:
1)
;
(2.6)
2)
и
;
3)
тройка векторов
,
,
– правая.
Если
заданы координаты векторов
и
в ортонормированном базисе
,
то их векторное произведение вычисляется
по формуле
(2.7)
Свойства векторного произведения:
1)
;
2)
,
где
–
некоторое число;
3)
.
Векторы
и
называются коллинеарными, если угол
между ними равен 0 или
радиан (
или
),
т.е. они лежат на параллельных прямых
или на одной прямой. Условие коллинеарности
векторов
и
:
если существует такое число
,
что
,
т.е. соответствующие координаты
коллинеарных векторов пропорциональны.
Векторное произведение коллинеарных
векторов
и
равно нулю:
Геометрический смысл векторного произведения: модуль векторного произведения векторов и численно равен площади параллелограмма, построенного на векторах и как на сторонах:
.
(2.8)
Смешанным
произведением векторов
,
,
называется число
.
Если
в произвольном правом ортонормированном
базисе
заданы координаты векторов
,
и
,
то
.
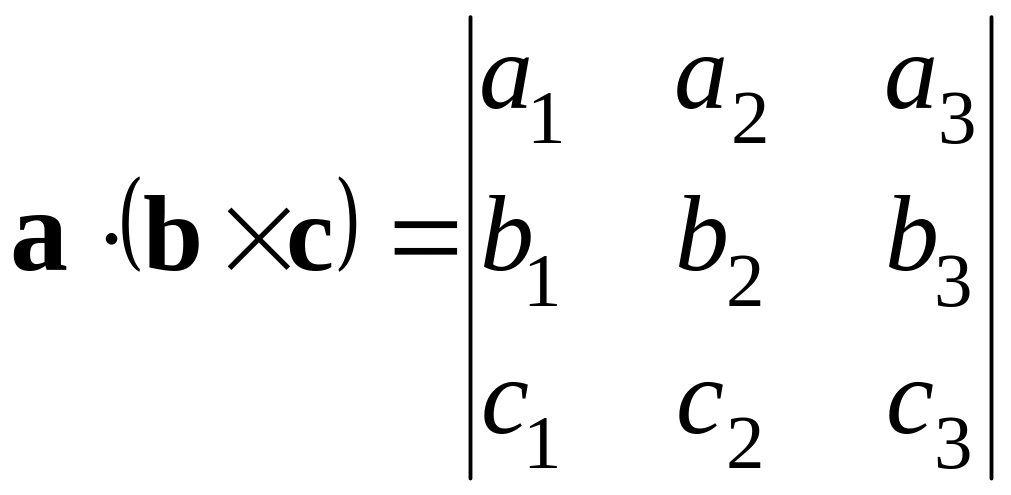(2.9)
Свойства смешанного произведения:
1)
;
2)
;
3)
если
,
то тройка векторов
,
,
– правая, если
– левая;
4)
.
Векторы , называются компланарными, если они лежат на параллельных плоскостях или на одной плоскости.
Условие
компланарности векторов
,
,
:
три вектора
,
,
компланарны тогда и только тогда, когда
их смешанное произведение равно нулю:
Геометрический смысл смешанного произведения: модуль смешанного произведения векторов , , численно равен объему параллелепипеда, построенного на векторах , , как на сторонах:
.
(2.10)
Пример
2.1. Даны две точки
,
.
Найти координаты вектора
и координаты точки
– середины отрезка
.
Решение.
По формуле (2.1) получаем
.
Пусть
,
тогда
,
,
.
Таким образом координаты точки
.
Пример
2.2. Даны два вектора
,
.
Найти угол между ними.
Решение. По формуле (2.5) получаем
,
тогда
.
Пример
2.3. Доказать, что векторы
,
ортогональны.
Решение.
По формуле (2.4) находим:
.
Согласно критерию ортогональности
векторы
и
ортогональны.
Пример
2.4. Даны два вектора
,
.
Найти векторное произведение
.
Решение. По формуле (2.7) получаем
.
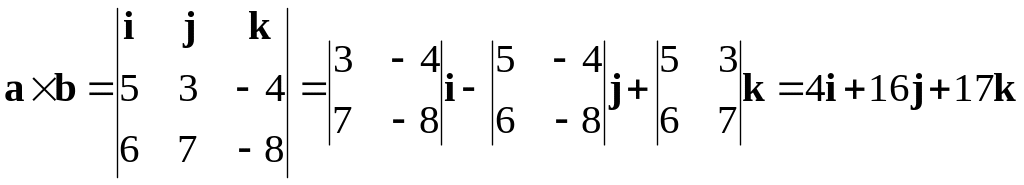Следовательно,
.
Пример
2.5. Вершины треугольника находятся
в точках
,
,
.
Вычислить площадь треугольника.
Решение.
Используя формулу (2.1), находим координаты
векторов
и
:
,
.
Далее, по формуле (2.7) определим
:
.
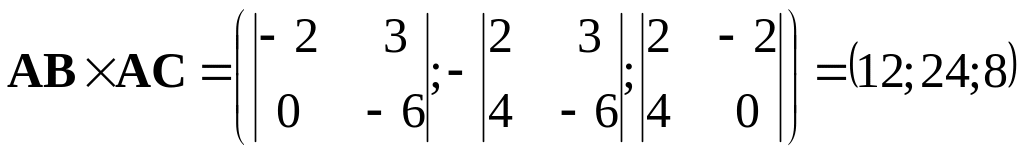Тогда
Пример
2.6. Вычислить, при каких значениях
и
векторы
и
коллинеарны.
Решение. Соответствующие
координаты коллинеарных векторов
пропорциональны, т.е.
,
откуда находим
и
.
Пример
2.7. Найти объем параллелепипеда,
построенного на векторах
,
,
.
Решение.
По формуле (2.10)
.
Используя формулу (2.9), находим:
.
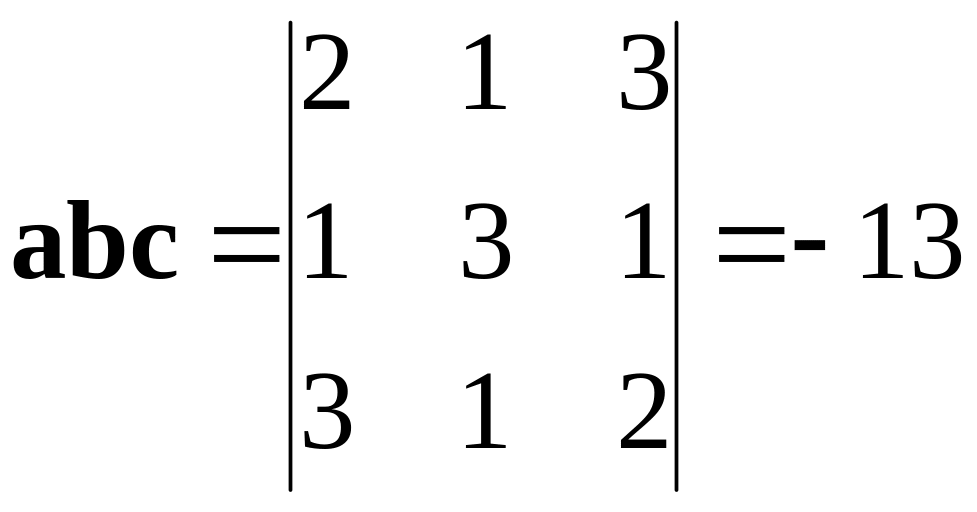Следовательно,
.
Пример
2.8. Доказать, что векторы
,
,
компланарны.
Решение. Проверим
выполнение условия компланарности. Так
как
,
то можно утверждать, что данные векторы
компланарны.
Пример
2.9. Вычислить объем треугольной
пирамиды, вершины которой находятся в
точках
,
,
,
.
Решение.
Используя формулу (2.1) найдем координаты
векторов, на которых построена пирамида:
,
,
.
Пример
2.10. Выяснить, лежат ли точки
,
,
,
в одной плоскости.
Решение.
Используя формулу (2.1) найдем координаты
векторов:
,
,
.
Теперь проверим выполнение критерия
компланарности. Так как
,
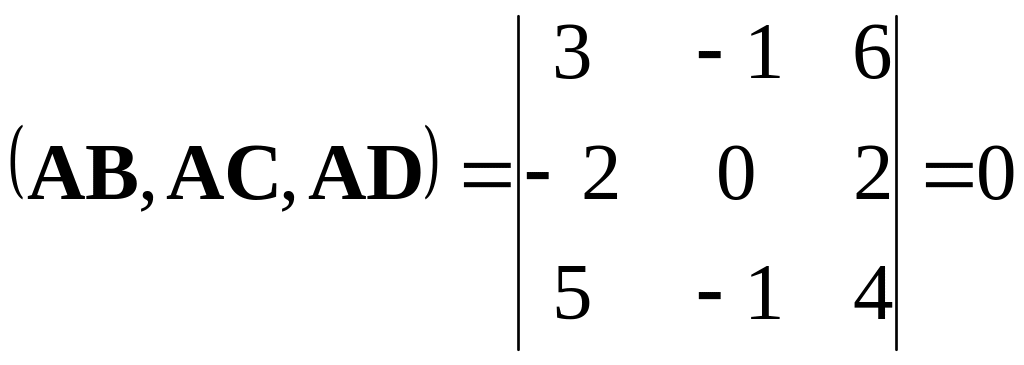то векторы компланарны, а значит, точки
,
,
,
лежат в одной плоскости.
Пример
2.11. Выяснить, правой или левой будет
тройка векторов
,
,
.
Решение.
Воспользуемся формулой (2.9):
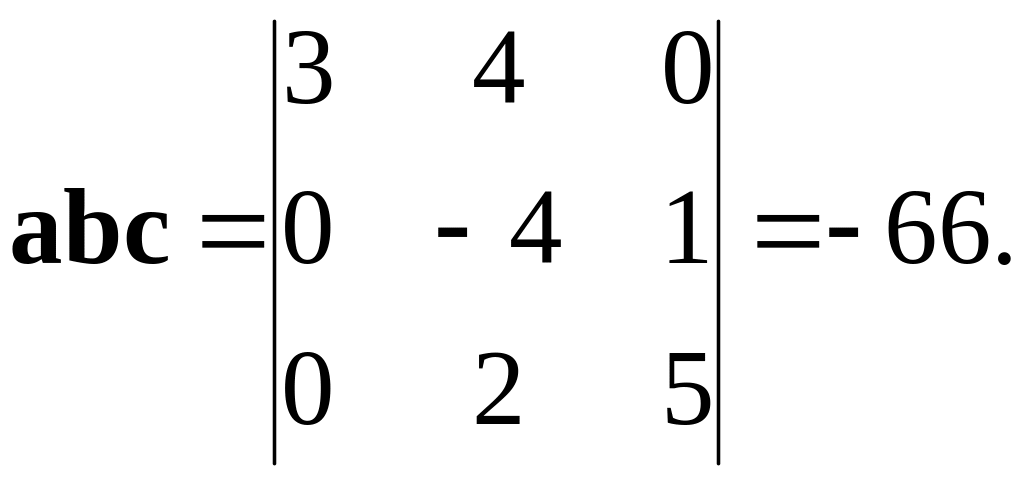
Согласно свойствам смешанного произведения, знак «–» указывает на то, что вектора , , образуют левую тройку.