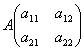1. Множества. Основные алгебраические структуры.
X, Y - множества, если к каждому элементу из множества X сопоставим единственный элемент множества Y, то такое сопоставление элементов называется функцией, либо отображением множества X на множество Y.
Операцией на множестве X называется функция, которая действует из множества X на X на множество Y, которое сопоставляется элементам X1, X2 на элементах Y.
Пример: 
Операция называется ассоциативной, если выполняется следующее свойство:
° - разл. операции (умножение, сложение и т.д.)
Операция называется
биективной, если выполняется равенство:
Операция называется
операцией с единицей, если для любого
элемента множества X
сущ. единственный элемент такой, что:
Полугруппой называется множество, в котором задана ассоциативная операция с единицей.
Полугруппа называется
группой, если для любого элемента x
из этой полугруппы сущ. обратный элемент,
т.е. 
Группа называется
абелевой, если для любого элемента
выполняется свойство коммутативности:
Кольцо:
Кольцо называется
телом, если операция умножения обратима
(относительно операции умножения сущ.
обратный элемент)
Коммутативное
тело-поле, если выполняется коммутативность
относительно умножения: 
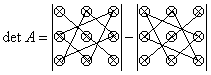
3. Определители квадратных матриц, их вычисление.
Определитель - число, которое записано в виде квадратной таблицы.
5. Невырожденная матрица. Обратная матрица. Свойства обратной матрицы.Будем считать, что все матрицы квадратные.
Матрица B называется правой обратной матрицей, если A·B=E
Матрица C называется левой обратной матрицей, если A·C=E
Если матрица A - квадратная и ее определитель отличен от 0, то тогда правая обратная матрица будет совпадать с левой обратной матрицей: B=C=A
Док-во: Если матрица B является правой обратной матрицей, то справедливо A·B=E, если матрица C является левой обратной матрицей, то C·A=E
C=C·E=C·A·B
A-1 - обратная матрица
Квадратная матрица называется невырожденной, если ее определитель отличен от 0.
Теорема о существовании обратной матрицы: A - квадратная матрица, тогда обратная матрица существует тогда, когда матрица A является невырожденной.
Док-во: Если A-1 - существует, это значит, что A·A-1=E, det(A·A-1)=detE
detA·detA-1=1 => detA≠0 - явл. невырожденной
Свойства обратной матрицы:
1° 
2° 
3° 
4° 
Невырожденной называется квадратная матрица, определитель которой не равен нулю. Квадратная матрица называется вырожденной, если ее определитель равен нулю.
Квадратная
матрица 
называется обратной к
невырожденной матрице 
,
если 
,
где 
-
это единичная матрица соответствующего
порядка.
7. Системы линейных алгебраических уравнений. Решение систем матричным методом.
Система уравнений - это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Решением системы уравнений называется упорядоченный набор чисел - значений неизвестных, при подстановке которых каждое уравнение системы обращается в верное равенство.
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
Упорядоченный
набор значений 
называется решением
системы,
если при подстановке в уравнения все
уравнения превращаются в тождество.
СЛАУ называется совместной, если она имеет, хотя бы одно решение. В противном случае система называется несовместной.
Пример: Система явл-ся совместной, так как она имеет, по крайней мере, одно решение.
Система явл-ся несовместной, так как выражения, стоящие в левых частях уравнений системы равны, но правые части не равны друг другу. Система называется определённой, если она совместна и имеет единственное решение. В противном случае (т.е. если система совместна и имеет более одного решения) система называется неопределённой.
Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.
Система называется квадратной, если количество уравнений равно количеству неизвестных.
Исходную СЛАУ можно записать в матричном виде:
,
где
матрица 
называется матрицей
системы,
это матрица,
составленная из коэффициентов при
неизвестных; 
- вектором-столбцом
неизвестных, 
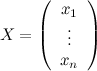- вектором-столбцом
правых частей или свободных
коэффициентов.
Расширенной
матрицей системы 
называется
матрица, полученная из матрицы системы
,
дописыванием справа после вертикальной
черты столбца свободных членов.
Матричный метод решения
Запишем заданную систему в матричном виде:
Если матрица
невырождена,
то тогда с помощью операций
над матрицами выразим
неизвестную матрицу 
.
Операция деления на множестве матриц
заменена умножением на обратную матрицу,
поэтому домножим последнее равенство
на матрицу
слева:
Поэтому, чтобы найти неизвестную матрицу надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
9. Решение систем линейных уравнений методом Гаусса.
Принцип метода Гаусса
Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный - методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных.
Метод Гаусса идеально подходит для решения систем содержащих больше трех линейных уравнений, для решения систем уравнений, которые не являются квадратными (чего не скажешь про метод Крамера и матричный метод). То есть метод Гаусса - наиболее универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система имеет бесконечно много решений или несовместна.