17. Нечеткие числа. Основные определения и операции.
Нечеткое число – нечеткое множество реальных чисел с нормальной выпуклой и непрерывной функцией принадлежности.
Выпуклая функция – описывается непрерывной производной и не имеет min и max.
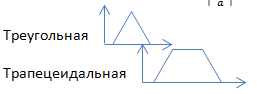
Обычно, для представления нечетких значений используют Гаусовскую , колоколообразную, треугольную, трапецеидальную функции
Гаусовская
функция описывается формулой
Колоколообразная
α
срезом(сечением) HM
–
называют четкое подмножество
универсального множества, для которого
значение функции принадлежности ≥α
Степенью НМ называется НМ для которого значение функции принадлежности которой для каждого значения из носителя равно µist
Концентрация – квадрат
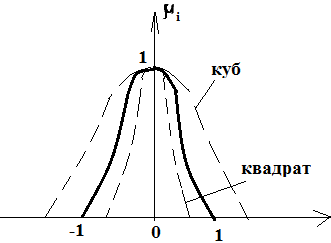
Пример: высокая температура, очень высокая, очень-очень
12. Методы поиска решений в продукционной модели.
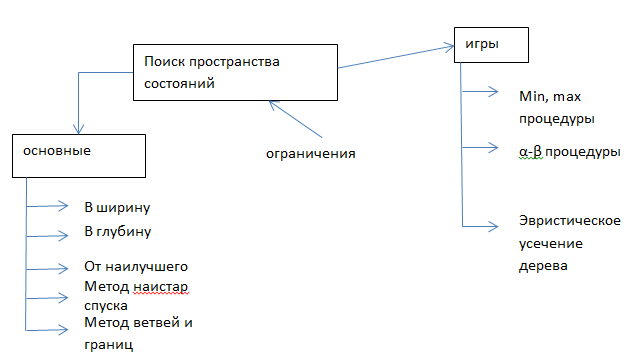
Метод наискорейшего спуска – повышение эффективности поиска, за счет упорядочения ветвей, вводится критерий оценки перспективности начального шага.
Особенность игр в том – действия выполняются при наличии противника.
На практике используют числа, которые называются статистической оценкой и характеризуют качество хода.
------- указывает на преимущество одного игрока, отрицая другого игрока.
В абсолютных величинах числа соответствуют преимуществу в ходе. В отрицательном с учетом знака преимущества игрока.
Min – преимущество одного
Max – другого
Выбор хода производится с учетом выбора противника при следующем ходе:
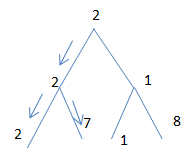
Сложность – вычисление оценки вершин, необходимых генерации всех возможных путей.
Метод α-β – уменьшение дерева решений, которое строится на основе статистических оценок.
Есть первый ход, который на 80% обеспечивает часть дерева решений.
5.Исчисление предикатов. Метод резолюции.
Исчисление высказываний не дает возможности выразить многие факты и рассуждения, которые пользуются в обыденной жизни. Можно обобщить исчисл. высказываний введя предложения - параметры.
Предикат - это функция одного или нескольких аргументов с булевскими значениями F или T. Тогда, если имеется выражение Макпост (М80852)=Т, Макпост(кофе)=F, стоитменьше5(М80852)=T.
Введение параметра увел. область применения исчисления высказываний; эффект введения параметров сравним с вводом массивов в язык программирования. Мы будем рассматривать предикаты 1-го порядка. Эти высказывания, отнесенные к объектам определенного типа. Синтаксические правила, аксиомы и правила вывода предикатов 1-го порядка полностью включает в себя правила исчисления высказываний.
Предикаты могут быть одноместными и многоместными.
Одноместные или унарные предикаты выражают св-ва объекта. Причем P(x) - P-св-во, X - объект, принимает 2 значения T (св-во выражается) F (нет).
Красное (яблоко) = T, необходим (компьютер).
Многоместные предикаты означ. отношения, которые существ. между элементами или группами элементов. Q(x,y)- Q-св-во, x и y - группы элементов.
В исчисление предикатов входят также символы функций, задаваемых на множестве прендметных переменных.
Например, Q=f(x) - может означать N квартиры, в которых есть телефон.
Предикаты типа P(x,y,z) назыв. атомарными. При помощи связок они образуют сложные формулы
P(x)[Q(X,Y) R(X,Z)]
Об истинности либо ложности этой формулы нельзя ничего сказать, если не указаны значения переменных x и y