6. Извлечение результата на основе метода резолюции.

Метод резолюции можно применить к КНФ. Пример:

R(x, y)\/Q(z, y)\/W(x, U)

┐R(10, 20)\/U(20, 50)

Если есть отрицательный и положительный резолент – 2 одинаковых предиката с разными знаками. Сделаем подстановку

R(10, 20)\/Q(z, 20)\/W(10, U) -> Q(z, 20)\/W(10, U)\/U(20,50)

Если противоречие найдено, то резудьтат решения – да. Если решение не найдено, решение может быть, но мы можем его не знать.

Задача. Известно, что палец – часть кисти, рука – часть человека, доказать, что палец – часть человека. Кисть – часть руки.

Р(п, к), Р(к, р), Р(р, ч) = Т(истина)

Р(п, ч)

Предположим, что это не так, тогда истина - ┐Р(п, ч).

Нужны правила: сокращение по ссылке, цепное. Известно, что Р(x, y)/\P(y, z), то Р(x, z)

Нужно удалить импликацию А-> B ≡ ┐A\/B

┐(P(x, y)/\P(y, z))\/P(x, z)

Применим закон де Моргана

┐P(x, y)\/┐P(y, z)\/P(x, z)

Получим дизъюнкт

1.P(x, z)\/┐P(x, y) \/ ┐P(y, z)

2.P(п, к) 3.Р(к, р) 4.Р(р, ч) 5.┐Р(п, ч)

Применяя метод резолюции получить противоречия, пустой дизъюнктор

Q1: x=п, y=к

1) Р(п, z)\/┐Р(п, к)\/┐Р(к, z)

2)Р(п, к)

Р(п, z)\/┐Р(к, z)

Q2: z=ч

1)Р(п, ч) \/ ┐Р(к, ч) 2)┐Р(п, ч)

┐Р(к, ч)

Q3: x=к, y=р

1)Р(к, z)\/┐Р(к, р)\/┐Р(р, z) 2)Р(к, р)

Р(к, z) \/ ┐Р(р, z)

Q4: z=ч

1)Р(к, ч)\/ ┐Р(р, ч) 2)Р(р, ч)

Р(к, ч) – пустой дизъюнкт

1)Есть ли книги Пушкина в библиотеке?

2)Какие книги есть Пушкина?

В(а, н)

В(Пушкин, ‘P&L’)

В(Пушкин, _ ) -количество аргументов: 1-Пушкин, _ - неопределен.

В(Пушкин, Х) Х = ‘P&L’

При работе системы строится дерево опровержения, приводящее к пустому дизъюнктору. На 1 этапе выбирается 1 цель. На 2 этапе, если найден пустой дизъюнкт, то получаем ответ «да», и необходимо извлечь переменные, при котором сущ. ответ на этот вопрос.

Пример: Если Джим ходит туда же куда и Джон, а Джон сейчас в школе, то где Джим.

В(Джон, х) -> В(Джим, х)

В(Джон, школа), В(Джим, х) х-?

┐В(Джон, х)\/ В(Джим, х)

В(Джон, школа), ┐В(Джим, х)

Смотрим дерево опровержения. Берется отрицание цели.

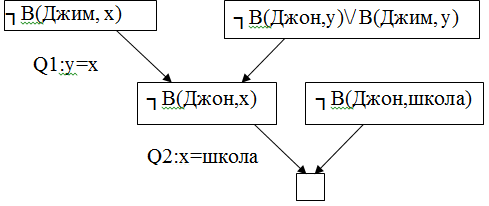
1)К каждому предложению, возникающему из целевого дизъюнкта добавляется его собственное отрицание.

2)Следуя структуре дерева опровержения выполняются те же операции, что и ранее.

3)В корневой вершине формируется ответ

7.Унификация. Процедура нахождения решения.

Применение поднятых правил логического вывода связано с необходимостью поиска подстановок, в результате которых различные логические выражения становятся идентичными. Этот процесс называется унификацией и является ключевым компонентом любых алгоритмов вывода в логике первого порядка. Алгоритм Unify принимает на входе два высказывания и возвращает для них унификатор, если таковой существует:

Рассмотрим несколько примеров того, как должен действовать алгоритм Unify. Предположим, что имеется запрос Knows {John, χ) — кого знает Джон? Некоторые ответы на этот запрос можно найти, отыскивая все высказывания в базе знаний, которые унифицируются с высказыванием Knows {John ,x). Ниже приведены результаты унификации с четырьмя различными высказываниями, которые могут находиться в базе знаний.

Последняя попытка унификации оканчивается неудачей (fail), поскольку переменная χ не может одновременно принимать значения John и Elizabeth. Теперь вспомним, что высказывание Knows {x, Elizabeth) означает "Все знают Элизабет", поэтому мы обязаны иметь возможность вывести логически, что Джон знает Элизабет. Проблема возникает только потому, что в этих двух высказываниях, как оказалось, используется одно и то же имя переменной, х. Возникновения этой проблемы можно избежать, стандартизируя отличие (standardizing apart) одного из этих двух унифицируемых высказываний; под этой операцией подразумевается переименование переменных в высказываниях для предотвращения коллизий имен. Например, переменную χ в высказывании Knows (x, Elizabeth) можно переименовать в z17 (новое имя переменной), не меняя смысл этого высказывания. После этого унификация выполняется успешно: