23. Архитектура и назначение многослойных нейронных сетей

Вероятно, архитектура многослойных нейронных сетей используется сейчас наиболее часто. Она была предложена в работе в 1986 году и подробно обсуждается почти во всех учебниках по нейронным сетям. Обычно сеть состоит из множества сенсорных элементов (входных узлов), которые образуют входной слой; одного или нескольких скрытых слоев вычислительных нейронов и одного выходного слоя нейронов.

В литературе нет единообразия относительно того, как считать число слоев в многослойных нейронных сетях. Одни предлагают считать число слоев, включая несуммирующий входной слой, другие – считать, только слои, выполняющие суммирование. Мы предлагаем использовать последнее определение. Согласно этому определению, многослойная нейронная сеть на рисунке ниже рассматривается как двухслойная. Вход распределительного слоя считается нулевым слоем.

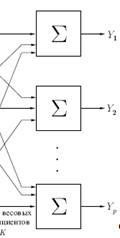
Пример 2-слойной н.с.

Многослойная нейронная сеть может моделировать функцию практически любой степени сложности, причем число слоев и число элементов в каждом слое определяют сложность функции. Определение числа промежуточных слоев и числа элементов в них является важным вопросом при конструировании.

Среди многослойных нейронных сетей можно выделить четыре наиболее значимых и важных класса нейронных сетей:

• сети прямого распространения – все связи направлены строго от входных нейронов к выходным. Такие сети еще называют многослойным персептроном, по аналогии с обычным персептроном Розенблатта, в котором только один слой;

• реккурентные нейронные сети или сети обратного распространения – сигнал в таких сетях с выходных нейронов или нейронов скрытого слоя частично передается обратно на входы нейронов входного слоя;

• радиально базисные функции – вид многослойной нейронной сети, имеющий скрытый слой из радиальных элементов и выходной слой из линейных элементов. Сети этого типа довольно компактны и быстро обучаются. Радиально базисная сеть обладает следующими особенностями: один скрытый слой, только нейроны скрытого слоя имеют нелинейную активационную функцию и синаптические веса входного и скрытого слоев равны единицы;

• самоорганизующиеся карты или сеть Кохонена. Такой класс многослойных нейронных сетей, как правило, обучается без учителя и успешно применяется в задачах распознавания. Сети такого класса способны выявлять новизну во входных данных: если после обучения сеть встретится с набором данных, непохожим ни на один из известных образцов, то она не сможет классифицировать такой набор и тем самым выявит его новизну. Сеть Кохонена имеет всего два слоя: входной и выходной, составленный из радиальных элементов.

24.Самоорганизующаяся сеть Кохонена: назначение и алгоритм.

Существует несколько основных методов разбиения множества объектов на группы. В данной статье описан кластеризатор на основе нейронной сети Кохонена.

Искусственная нейронная сеть Кохонена [1] или самоорганизующаяся карта признаков (SOM) была предложена финским исследователем Тойво Кохоненом в начале 1980-х годов.

Рис.1: топология нейронной сети Кохонена

Она представляет собой двухслойную сеть (рис.1). Каждый нейрон первого (распределительного) слоя соединен со всеми нейронами второго (выходного) слоя, которые расположены в виде двумерной решетки.

Нейроны выходного слоя называются кластерными элементами, их количество определят максимальное количество групп, на которые система может разделить входные данные. Увеличивая количество нейронов второго слоя можно увеличивать детализацию результатов процесса кластеризации.

Функционирование сети

Система работает по принципу соревнования [2] -- нейроны второго слоя соревнуются друг с другом, побеждает тот элемент-нейрон, чей вектор весов ближе всего к входному вектору сигналов. За меру близости двух векторов обычно берётся евклидово расстояние между ними. Таким образом, каждый входной вектор относится к некоторому кластерному элементу.

Обучение сети

Прежде чем сеть начнет работать её необходимо обучить на множестве данных, которое будем кластеризировать.

Для обучения сети Кохонена используется соревновательный метод [1,2]. На каждом шаге обучения из исходного набора данных случайно выбирается один вектор. Затем производится поиск нейрона выходного слоя, для которого расстояние между его вектором весов и входным вектором - минимально.

По определённому правилу производится корректировка весов для нейрона-победителя и нейронов из его окрестности, которая задаётся соответствующей функцией окрестности h(t,j,m), где m - нейрон-победитель, j - нейрон выходного слоя для которого вычисляем значение функции окрестности, t - параметр времени. Радиус окрестности должен уменьшаться с увеличением параметра времени .

В данном случае в качестве функцией окрестности была использована функция Гаусса (1). 

Рис.2: функция Гаусса (1)

Алгоритм обучения сети Кохонена выглядит следующим образом:

1. Инициировать матрицу весов малыми случайными значениями (на отрезке [-1,1]).

2. Случайным образом выбрать вектор из входного множества.

3. Для каждого выходного нейрона j вычислить расстояние (2) между его вектором весов w_j и входным вектором x :

(2)

4. Найти выходной нейрон-победитель j_min с минимальным расстоянием (2) 

min( d_j )

5. Для выходного нейрона-победителя j_min и для его соседей из окрестности (1) обновляются векторы весов по правилу (3).

w_ij(t+1)=w_ij(t) + e(t) ^. h(t,j,m) ^. (x_i-w_ij(t))(3)

Здесь:

• w_ij(t) - значение весового коэффициента связи входного нейрона i и выходного нейрона j в момент времени t

• h(t,j,m) - значение функции окрестности с центральным нейроном выходного слоя m для нейрона выходного слоя j в момент времени t

• e(t) - коэффициент скорости обучения в момент времени t

• x_i - выход нейрона первого слоя номер i.