19 Вопрос. Доказательство несмещенности и состоятельности выборочного среднего. Исправленная выборочноая дисперсия.

Несмещенной называют статистическую оценку Θ∗, математическое ожидание которой равно оцениваемому параметру Θ при любом объеме выборки, т. е. M[Θ∗] = Θ

В теории ошибок измерений систематическими ошибками называют неслучайные ошибки, искажающие результаты измерений в одну определенную сторону. Например, измерение длины растянутой рулеткой систематически дает заниженные результаты.

Определение 43. Смещенной называют оценку, математическое ожидание, которой не равно оцениваемому параметру. Ошибочным считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Действительно, возможные значения Θ∗ могутбыть сильно рассеяны вокруг своего среднего значения, т е. дисперсия D[Θ∗] может быть значительной. В этом случае найденная по данным одной выборки оценка, например Θ∗1, может оказаться весьма удаленной от среднего значения Θ∗, а значит, и от самого оцениваемого параметра Θ; приняв Θ∗1в качестве приближенного значения Θ, допустили бы большую ошибку. Если же потребовать, чтобы дисперсия Θ∗ была малой, то возможность допустить большую ошибку будет исключена. По этой причине к статистической оценке предъявляется эффективности.

Состоятельной называют статистическую оценку, которая при n → ∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n → ∞ стремится к нулю, то такая оценка будет и состоятельной.

20. Точечные статистические оценки параметров распределения. Метод моментов и метод наибольшего правдоподобия для дискретного и непрерывного случаев. Примеры.

Метод max правдоподобия – выражает плоность вер-сти совместного появления результатов выборки х1, Х2,..., хn: L(x1, x2,…xi…xn; θ)=φ(x1,θ)*φ(x2,θ)…φ(xi,θ)…φ(xn, θ). Исследуем ф-я на max и min. Для этого исслед-ся ln (L(θ)). D lnL\dθ=0 – находим θ₀; d^2lnL\dθ – если <0 – то max, тогда θ= θ₀

Метод моментов - определ-е кол-во выборочных моментов (начальных ν_k или центральных моментов μ_k, или тех и других) приравнивается к соответствующим теоретич-м моментам р-я сл вел X. ν_k=∑Xi^k *pi, μ_k=∑(Xi-M(X))^kpi.

21. Доверительные интервалы, доверительная вероятность. Построение доверительных интервалов для математического ожидания нормального распределения (с известной дисперсией).

Пусть x_1, x_2,…,x_n — выборка из некоторого распределения с плотностью распределения p(x; θ), зависящей от параметра θ. Задача состоит в том, чтобы построить для θ доверительный интервал.

Опр: Интервал 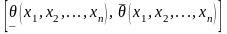называется доверительным, если с вероятностью (1-α) неизвестный параметр θ попадает в этот интервал. Тогда (1-α) — доверительная вероятность.

Доверит. интервал для a при известном параметре σ.

Пусть x_1, x_2,…,x_n — выборка из N(a, σ), причем a неизвестно, а σ известно.

Построить доверительный интервал для a при заданной доверительной вероятности (1- a).

Для решения задачи воспользуемся следующим фактом.

Пусть X₁, X₂, X_n, — независимые случайные величины, распределение которых нормально с параметрами a и σ. Тогда случайная величина нормальна с параметрами a и . Для обоснования этого утверждения достаточно вычислить плотность распределения .

Статистика имеет нормальное распределение с параметрами (0,1)(стандартное нормальное распределение). Пусть — квантиль порядка стандартного нормального распределения. Тогда , следовательно

. Таким образом статистики задаются равенствами , , и доверит. интервал для a построен.

22. Доверительные интервалы для дисперсии нормально распределенной случайной величины)Доверит интервал для дисперсии. , , - р-е хи квадрат

22 Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной надёжностью γ покрывает заданный параметр.

Интервальной оценкой (с надёжностью γ) математического ожидания а нормального распределённого количественного признака по выборочной средней х_в

1. при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал х_в – t (σ/√n) < a < х_в + t (σ/√n), где δ = t (σ/√n) – точность оценки, n – объём выборки, t – значение аргумента функции Лапласа Ф(t), при котором Ф(t) = γ/2.

2. при неизвестном σ (и объёме выборки n < 30) х_в – t_γ (s/√n) < a < х_в + t_γ (s/√n), где s – исправленное выборочное среднее квадратическое отклонение, t_γ находят по таблицам распределения Стьюдента по заданным n (число степеней свободы k = n – 1) и γ.

Интервальной оценкой (с надёжностью γ) среднего квадратического отклонения σ нормально распределённого количественного признака Х по исправленному выборочному среднему квадратическому отклонению s служит доверительный интервал s (1 – q) < σ < s (1 + q) (при q < 1), 0 < σ < s (1 + q) (при q > 1), где q находят по таблицам распределения χ² по заданным n и γ.