12. Непрерывные случайные величины. Вычисление математического ожидания и дисперсии для равномерно и нормально распределенных случайных величин

Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [а, b] если ее плотность вероятности ϕ(х) постоянна на этом отрезке и равна 0 вне его, т.е.

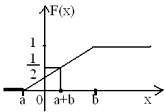
при Кривая распределения ϕ(х) и график функции распределения F(х) случ величины Х приведены на рис.

Теорема: Функция распределения случайной величины Х распределенной по равномерному закону, есть . Ее математическое ожидание а дисперсия

Н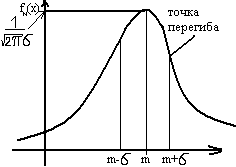 епрерывная случайная величинаХ имеет нормальный закон распределения с параметрами а и σ ², если плотность вероятности имеет вид:

Теорема: Математическое ожидание случ.величины Х распределенной по нормальн закону, равно параметру a этого закона, т.е. M(x)=a а ее дисперсия – параметру σ ², т.е. D(x)= σ ²

Опр.2 Нормальное распределение с параметром N(0,1) наз-ся стандартным нормальным распределением.

; Т.о. случ-я вел-на z имеет станд. нормалное распределение

13. Функция распределения непрерывной случайной величины и ее свойства. Функция

плотности распределения. Мода, медиана. Начальные и центральные моменты. Примеры

Опр.1 Случ. вел-на Х наз-ся непрерывной, если её ф-ия распределения F(X) непрерывна в любой точке числовой прямой и диф-ма всюду, кроме, быть может, отдельных точек, где она терпит излом.

Опр.2. Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения: f(x) = F'(x).

Функция плотност и вероятностей непрер случ величины Х назыв производная от её функции распределения

Свойства плотности вероятности.

Свойство 1. Плотность распределения неотрицательна, т.е. f(x) ≥ 0. (как производная неубывающей ф-ии распределения)

Свойство 2. Вер-ть попадания непрер-ой случ. вел-ны в равна

Док-во: . Но т.к ф-я распред-я явл-ся первообразной для плотности (по опред.), то по ф-ле Ньютона-Лейбница, приращ-е первообразной на отрезке – это и есть опред-ый интеграл.

Свойство 3. Ф-ия распределения непрер-ой случ. вел-ны равна F(x) = ∫^х_–∞ f(x)∙dx. Док-во: F(X)=P{X<x}=P{– <X<x} и по св-ву 2 следует св-во 3.

Свойство 4. Несобственный интеграл от плотности распределения в пределах от -∞ до +∞ равен единице: ∫^+∞_-∞ f(x)∙dx = 1. Док-во: рассм-м

Опр.6. Модой М₀(Х) непрерывной случайной величины Х называют ее наиболее вероятное значение

Опр.8. Медианой М_е(Х) непрерывной случайной величины Х называют то её возможное значение, которое определяется равенством: Р[X < М_е(Х)] = P [ X > М_е(Х)]=1/2

Геометрически медиану можно истолковать как точку, в которой ордината f(x) делит пополам площадь, ограниченную кривой распределения.

С понятием квантиля тестно саязано понятие процентной точки. Под 100%-ной точкой подразумевается квантиль Х_1-q т.е. такое значение случ величины Х при котором P(X>= Х_1-q)=q

Начальным моментом k- го порядка случайной величины Х называется мат.ожидание k- ой степени этой случайной величины

Центральным моментом порядка k случ.величины Х называется мат ожидание k степени отклонения этой случайной величины от ее мат ожидания

Начальным моментом 1-го порядка V1=M(x)-мат. Ожид.

Центральн момент 1-го порядка

Центральный момент 2-го порядка - дисперсия

Аналогично центральным моментам более высок.порядков выраж.через начальные моменты.

Центральный момент 3-го порядка характеризует ассиметрию кривой распределения.

Ассиметрия.

, G- среднеквадратичное отклонение

Центральный момент характеризует крутизну кривой.

Безразмерная величина - коэффициент эскцесса

Для кривой нормального распределения

Для нормальной кривой E=0

14.Понятие о законе больших чисел. Неравенство Чебышева (с доказательством). Закон

больших чисел в схеме Бернулли.

Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.

Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.

Неравенство Чебышева: Для любой случайной величины, имеющей мат ожидание и дисперсию, справедливо неравенство Чебышева: где a=M(x)

Неравенство Чебышева для некоторых случайных величин:

1.для случ величины Х=m? Имеющей биномиальный закон распределения с мат ожиданием а=M(x)=np и D(x)=npq

2/для частости m\n события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью a=M(m\n)=p и имеющей дисперсию D(m\n)=pq\n

Закон больших чисел Бернулли.

Пусть производится последовательность независимых испытаний, в результате каждого из которых может наступить или не наступить событие А, причем вероятность наступления этого события одна и та же при каждом испытании и равна р. Если событие А фактически произошло m раз в n испытаниях, то отношение m/n называют, как мы знаем, частотой появления события А. Частота есть случайная величина, причем вероятность того, что частота принимает значение m/n, выражается по формуле Бернулли (13):

Закон больших чисел в форме Бернулли состоит в следующем: с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом числе опытов частота появления события А как угодно мало отличается от его вероятности, т. е.

иными словами, при неограниченном увеличении числа n опытов частота m/n события А сходится по вероятности к Р(А). (Доказательство)

Мы говорили (см. § 1, п. 1), что при большом числе испытаний частота Р*(А)=m/n события А обладает свойством устойчивости. Это обстоятельство находит свое объяснение в законе больших чисел Бернулли.

15, Теорема Чебышева (с доказательством). Центральная предельная теорема Ляпунова (без

доказательства). Примеры.

Теорема Чебышева: Если дисперсии n независимых случайных величин х1, х2.. ограничены одной и той же постоянной то при неограниченном увеличении числа n средняя арифметич случайных величин сводится по вероятности к средней арифметич их мат ожиданий а1,а2,…

Следствие: Если независимые случайные величины х1,х2,..имеюют одинаковые математич ожидания =а, а их дисперсии ограничены одной и той же постоянной , то

Теорема Ляпунова.

Если Х1,Х2…независимые случайные величины, у каждой из которых существует мат ожидание M(Xi)=a , дисперсия D(Xi)= σ ² , абсолютный и центральный момент 3-го порядка M(|Xi-ai|³)=m_i и

То закон распределения суммы Yn=X1+X2+.. при n стремящемся к бескон. Неограниченно приближается к нормальному, с мат ожиданием и дисперсия

Следствие: Если Х1,Х2…независимые случайные величины, у которых существуют равные мат ожидания M(Xi)=a , дисперсия D(Xi)= σ ² и абсолютные и центральные моменты 3-го порядка M(|Xi-ai|³)=m_{i то} закон распределения суммы Yn=X1+X2+.. при n стремящемся к бескон. Неограниченно приближается к нормальному закону .

16.Основные понятия математической статистики: генеральная совокупность, выборка,

выборочные характеристики. Методы отбора.

Генеральная совокупность — совокупность объектов, из которых производится случайный выбор объектов для исследования.

Выборочная совокупность — отобранные случайным образом объекты из генеральной совокупности.

Характеристики выборки:

Качественная характеристика выборки – кого именно мы выбираем и какие способы построения выборки мы для этого используем.

Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.