9 Вопрос. Свойства математического ожидания и дисперсии дискретной случайной величины (с доказательствами).

Математическое ожидание случайной величины.

Математическим ожиданием случайной величины х (M[x])называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности появления тех или иных значений.

Для дискретной случайной величины

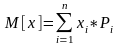
Для непрерывной

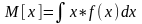
С механической точки зрения мат. Ожидание это абсцисса центра тяжести системы точек расположенных по одноименной оси. Размерность мат. Ожидания совпадает с размерностью самой случайной величины.

Математическое ожидание случайной величины всегда больше наименьшего значения и меньше наибольшего.

Дисперсия

Дисперсия (D[x]) характеризует рассеивание или разряженность случайной величины около ее математического ожидания.

Для дискретных

Для непрерывных

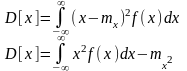
Дисперсия случайной величины всегда величина положительная

Размерность дисперсии равна квадрату разности случайной величины

Среднеквадратическое (стандартное) отклонение.

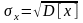
10. Биномиальное распределение, вычисление математического ожидания и дисперсии

биномиально распределенной случайной величины.

Биномиальное распределе­ние.

Биноминальным называют распределение вероятностей, определяемой формулой Бернулли Этот закон назван «биноминальным» потому, что правую часть равенства можно рассматривать как общий член разложения Бинома Ньютона:

Первый член разложения определяет вероятность наступления рассматриваемого события раз в независимых испытаниях …последний член определяет вероятность того, что событие не появится ни разу.

Можно записать Биноминальный закон в виде таблицы:

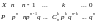
Опр. Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании: M(X) = np.

Опр. Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X) = npq.

11. Геометрическое распределение. Распределение Пуассона. Вычисление основных

числовых характеристик этих распределений.

Геометрическое распределение. Гипергеометрическое распределение.

Дискретная случайная величина Х=m имеет геометрическое распределение с парам P , если она принимает значения 1, 2,...m.. с вероятностями , где 0 < р < 1, q= р - 1

Случ величина X=m имеющая геометрич распределение, представляет собой число m испытаний, проведенных по схеме Бернулли, с вероятностью p наступления события в каждом испытании до первого положительного исхода.

Мат ожидание случ величины Х имеющей геометр распределение с парам P

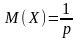
А дисперсия .

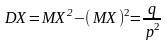Гипергеометрическое распределение

Дискретная случайная величина Х имеет гипергеометр распределение с параметрами n,M,N если она принимает значения 0,1,2, m,…min (n,M) с вероятностями , где M<=N, n<=N; n,M,N – натуральные числа

Мат ожидание случайной величины Х имеющей гипергеометрическое распределение с параметрами n,M,N есть а ее дисперсия

Гипергеометрическое распределение можно рассматривать как модификацию биномиального распределения для случая конечной совокупности, состоящей из N объектов,M из которых обладают этим свойством. Можно сказать что при N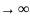 функция вероятнос тей гипергеом распределения стремится к соответствующей функции биномиального закона.

Закон распределения Пуассона. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона.

Дискретная случ величина Х имеет закон распределения Пуассона м параметром λ>0? Если она принимает значения 0,1,2,..m.. с вероятностями P(X=m) = λ^m e^-λ / m!, где m – число появлений события в n независимых испытаниях, λ = np (среднее число появлений события в n испытаниях),

Опр.6. Математическое ожидание распределения Пуассона равно произведению числа испытаний на вероятность появления события в одном испытании: M(X) = np = λ.

Опр.7. Дисперсия распределения Пуассона равна произведению числа испытаний на вероятность появления события в одном испытании, то есть равна математическому ожиданию: D(X) = np = λ.