
- •Элементы комбинаторики: перестановки, размещения сочетания. Примеры
- •Классическое определение вероятности, случайные события, элементарные исходы, свойства классической вероятности. Примеры.
- •Совместные и несовместные события. Теорема сложения вероятностей (док-во). Примеры.
- •4. Зависимые и независимые события. Теорема умножения вероятностей (док-во). Примеры.
- •5. Условная вероятность. Теорема о формуле полной вероятности, формулы Бейеса. Пример.
- •6. Понятие распределения вероятностей случайных событий. Схема независимых испытаний. Формула Бернулли. Повторные независимые испытания. Формула Бернулли с выводом.
- •7. Случайные величины: определение, функция распределения случайной величины и ее свойства, независимые случайные величины.
- •8. Определения числовых характеристик дискретных и непрерывных случайных величин: математическое ожидание, дисперсия, мода, медиана, центральные и начальные моменты.
- •9. Свойства математического ожидания и дисперсии дискретной случайной величины.
- •10. Биномиальное распределение, вычисление математического ожидания и дисперсии биномиально распределенной случайной величины.
- •11. Геометрическое распределение. Распределение Пуассона. Вычисление основных числовых характеристик этих распределений.
- •12. Непрерывные случайные величины. Вычисление математического ожидания и дисперсии для равномерно и нормально распределенных случайных величин.
- •13. Функция распределения непрерывной случайной величины и ее свойства. Функции плотности распределения. Мода, медиана. Начальные и центральные моменты. Примеры.
- •14. Понятие о законе больших чисел. Неравенство Чебышева (док-во).
- •15. Теорема Чебышева (док-во). Центральная предельная теорема Ляпунова (без док-ва). Примеры.
- •16. Основные понятия математической статистики: генеральная совокупность, выборка, выборочные характеристики. Методы отбора.
- •17. Статистические оценки и их свойства: несмещенность, эффективность, и состоятельность. Примеры.
- •21. Точечные статистические оценки параметров распределения. Метод наибольшего правдоподобия для дискретного и непрерывного случаев. Примеры.
- •25. Статистические гипотезы, постановка задачи построения критерия проверки статистической гипотезы. Уровень значимости и мощность критерия.
10. Биномиальное распределение, вычисление математического ожидания и дисперсии биномиально распределенной случайной величины.
Биноминальный з-н\
Дискретная случ. велич. X имеет биномиальный з-н с параметрами n и р, если она принимает значения 0, 1, 2,..., m,..., n с вероятностями P(X=m)=Cnmpmqn-m, где 0<p<1, q=1-p.


11. Геометрическое распределение. Распределение Пуассона. Вычисление основных числовых характеристик этих распределений.
З-н распред-я Пуассона. Дискретная случ. велич X имеет
Этот з-н с параметром λ > 0, если она принимает значения 0, 1, 2,..., m (бесконечное, но счетное множ-во значений) с вер-стями P(X=m)=λme- λ \m! . (n→∞, p→0).


Геометрическ распр-е.
Дискретная случ. велич Х=m имеет геометрическое р-е с параметром р, если она
принимает значения 1,2,..., m... (бесконечное, но счетное множ-во значений) с вер-стями P(X=m)=pqm-1, где 0<p<1, q=1-p. Теорема.(без док-ва) Если случ велич Х распределена по геометрич р-ю, то М(Х)=1\р, D(X)=q\p^2.
12. Непрерывные случайные величины. Вычисление математического ожидания и дисперсии для равномерно и нормально распределенных случайных величин.
Сл\в Х наз-ся непрерывной, если её Функция Распределения непрерывна в любой точке и дифференцируемая во всюду, кроме отдельных точек (точки излома).
Мат\ожиданием дискретной сл\в называется сумма произведений всех возможных значений сл\в на их вероятности.
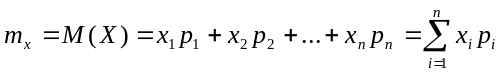 Мат\о
существует, если ряд, стоящий в правой
части равенства, сходится абсолютно. С
точки зрения вер-ти можно сказать, что
м\о приближенно = среднему арифметическому
наблюдаемых значений сл\в.
Мат\о
существует, если ряд, стоящий в правой
части равенства, сходится абсолютно. С
точки зрения вер-ти можно сказать, что
м\о приближенно = среднему арифметическому
наблюдаемых значений сл\в.
Пусть НСВ Х задана ФР F(x). Допустим, что все возможные значения сл\в принадлежат отрезку [a,b].
Мат\ож-м
НСВ Х,
возможные значения которой принадлежат
отрезку [a,b], наз-ся определенный интеграл
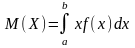 .
Если возможные значения сл\в рассм-ся
на всей числовой оси, то мат\о
нах по формуле:
.
Если возможные значения сл\в рассм-ся
на всей числовой оси, то мат\о
нах по формуле: ,
при этом предпол-ся, что несобственный
интеграл сходится.
,
при этом предпол-ся, что несобственный
интеграл сходится.
Дисперсией
НСВ наз мат\ож
квадрата ее отклонения.
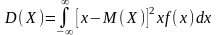 .
По аналогии с дисперсией, дискретной
сл\в, для практического вычисления
дисперсии используется формула:
.
По аналогии с дисперсией, дискретной
сл\в, для практического вычисления
дисперсии используется формула:
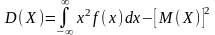 .
.
13. Функция распределения непрерывной случайной величины и ее свойства. Функции плотности распределения. Мода, медиана. Начальные и центральные моменты. Примеры.
Функция распределения НСВ:
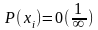 ,
в качестве способа задания НСВ используется
функция
распределения НСВ.
,
в качестве способа задания НСВ используется
функция
распределения НСВ.
ФРНСВ
наз вер-ть т\ч она примет значение меньшее
заданного.
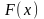 -обознач
ф-ии распр в-тей
-обознач
ф-ии распр в-тей
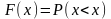
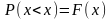
Основные свойства ф-ии распределения НСВ:
С1.
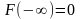 С2.
С2.
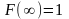
С3.
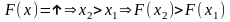
С4.
Вер-ть т\ч НСВ
примет значение из интервала, равна
приращению ф-ии на этом интервале
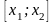
1 )
)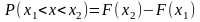
2)
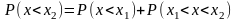

Скорость
изменения функции распределения хар-ся
плотностью распр-я. Обозначается символом
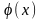 .
Плотностью вер-ти (плотностью распр-я)
НСВ
Х наз-ся производная её ф-ии распр-я
.
Плотностью вер-ти (плотностью распр-я)
НСВ
Х наз-ся производная её ф-ии распр-я
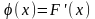
Свойства плотности распр-я (ПР):
С1.
ПР –
неотрицательная функция.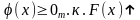 ;
;
С2.
Вер-ть попадания
НСВ в интервал [a,b]
равна определённому интегралу от её
плотности вер-ти в пределах от a
до b,
т.е.
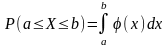
С3.
Ф-я распр НСВ
м\б выражена через плотность вер-ти по
формуле:
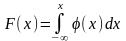
С4.
Несобственный интеграл в бесконечных
пределах от плотности вер-ти НСВ =1.
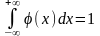
Мода Мо(Х) случ. величины X - наз-ся ее наиболее вероятное значение (для которого вер-сть рi или плотность вер-сти φ(х) достигает max). Медиана Ме(Х) непрерывной случ. величины X наз-тся такое ее значение, для которого Р(X<Me(X))=P(X>Me(X))=0,5, т.е. вер-сть того, что X примет значение, < Ме(Х) или > ее, одна и та же и = 0,5. Геометрически: вертикальная прямая, проходящая через точку х=Ме(Х), делит площадь фигуры под кривой распределения на 2 равные части. Начальным моментом k-го порядка случ. велич X наз-ся мат. ожидание k-й степени этой величины: νk=M(X^k). Для непрерывн случ велич: νk=∫х^k φ(x)dx (интеграл от -∞ до +∞). Центральный моментом k-го порядка случ. велич. X наз-тся матю ожидание k-й степени отклонения X от ее мат. ожидания: μk=M[X-M(X)]^k. Для непрерывной случ велич: μk= ∫(х-М(Х))^k φ(x)dx (интеграл от -∞ до +∞).
