1. Элементы комбинаторики: перестановки, размещения сочетания. Примеры

Комбинаторика – раздел матем-ки, изучающий, в частности, методы решения комбинаторных задач - задач на подсчет числа различных комбинаций.

Размещения из n элементов по m – если комбинации из n эл-тов по m отличаются либо составом эл-тов, либо порядком их расположения. Сочетания из n элементов по m - комбинации элементов отлич-ся только составом эл-тов, порядок не важен. 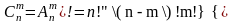(1)

Перестановки из n эл-тов - если комбинации эл-тов отличаются только порядком расположения эл-тов. Pn=n!

Размещения с повторениями – когда любой из эл-тов может быть использован любое число раз.

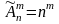
Сочетания с повторениями - любой из эл-тов может быть использован любое число раз. 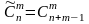(определяется по ф-ле 1, см.выше).

Перестановки с повторениями из n эл-тов - если в перестановках из общего числа n элементов есть k различных эл-тов, при этом 1-й эл-т повторяется n1 раз, 2-й эл-т - n2 раз, k-й эл-т - nk раз, причем n1+n2+…+nk=n. . Для непосредственного вычисления вер-сти используется ее классич-е определение P(A)=m\n.

2. Классическое определение вероятности, случайные события, элементарные исходы, свойства классической вероятности. Примеры.

Вероятность события - численная мера возможности наступления события.

Классическое определение - вероятность события А равна отношению числа случаев, благоприятствующих ему, к общему числу случаев, т.е. 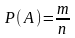, Р(А)- вер-сть соб. А; m - число случаев, благоприятствующих соб. А; n - общее число случаев. Следует рассматривать как метод вычисления вер-стей для испытаний, сводящихся к схеме случаев.

Свойства вероятности события: 1. 0 < Р(А) < 1; 2. Р(достоверного соб.) = 1; 3. Р(невозможного соб.) = 0.

Свойства событий: 1. Соб. должны быть исходами только тех испытаний, котор могут быть воспроизведены неогранич-ое число раз при одинаковых условиях. 2. Соб. должны обладать статистической устойчивостью (устойчивостью относительных частот – т.е. частость изменяется не значительно). 3. Число испытаний, в результате котор появляется соб. А, должно быть достаточно велико.

3. Совместные и несовместные события. Теорема сложения вероятностей (док-во). Примеры.

Два соб-я наз-ся несовместимыми, если 1 соб-е исключает появление другого.

Неск-ко соб-ий наз-ся попарно несовместимыми, если появл-е любого из этих соб-ий исключает появление других.

Сложение вероятностей зависит от совместности и несовместности событий.

Несовместные события.

Вер-ть суммы двух несовм соб А и В равна сумме вер-ей этих соб-й. Это вытекает из того, что множество С = А+В включает подмножества А и В, не имеющие общих точек, и Р(А+В) = Р(А)+Р(В) по опр вер-ти на основе меры. По частотному опр-ю вер-ти в силу несовместности соб-й имеем: P(A+B) = 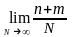= 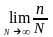+ 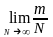= P(A) + P(B), где n и m - число случаев появления соб-й А и В соответственно при N испытаниях.

Противоположные события также являются несовместными и образуют полную группу. Отсюда, с учетом: P(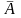 ) = 1 - Р(А). В общем случае для группы несовместных событий: P(A+B+...+N) = P(A) + P(B) + ... + P(N), если все подмножества принадлежат одному множеству соб-й и попарно несовм. А если эти подмножества образуют полную группу соб-й, то с учетом: P(A) + P(B) + ... + P(N) = 1

Совместные события. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: P(A+B) = P(A) + P(B) - P(AB).

Разобьем события А и В каждое на два множества, не имеющие общих точек: А', A'' и B', B''. Во множества А'' и B'' выделим события, появляющиеся одновременно, и объединим эти множества в одно множество С. Для этих множеств действительны выражения:

С = A''B''  А''  В''  АВ, P(C) = P(A'') = P(B'') = P(AB).

P(A) = P(A')+P(A''), P(A') = P(A)-P(A'') = P(A)-P(AB).

P(B) = P(B')+P(B''), P(B') = P(B)-P(B'') = P(B)-P(AB).

Множества A', B' и С попарно несовм : P(A+B) = P(A'+B'+C) = P(A') + P(B') + P(С).

В общем случае, для m различных событий А₁, А₂, ..., А_m:

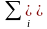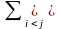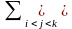P(A₁+...+ A_m) = P(A_i) - P(A_iA_j) + P(A_iA_jA_k) -...+(-1)^m+1P(A₁A₂ ... A_m).

Теорема сложения: Вер-ть суммы двух несовм-х соб-й = сумме вер-тей этих соб. P(A+B+…+К)=P(A)+P(B)+…+Р(К)

Доказательство: Пусть в рез-те испытания из общего числа n равновозможных и несовм-х исходов испытания соб-ю А благоприятствует m1 случаев, а соб-ю В – m2 случаев. Согласно классич определению P(A)=m1\n, P(В)=m2\n. Т.к соб А и В несовм-е, то ни 1 из случаев, благоприят-х 1 из этих соб-й, не благоприят-т другому. Поэтому событию А+В будет благоприятств-ть m1+m2 случаев, следовательно:

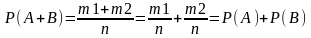
Следствие 1: Сумма вер-ей событий, образующих полную группу, равна 1: P(A)+P(B)+…+Р(К)=1, Если события А,В,…,К образуют полную группу, то они единственно возможные и несовместимые.

ТК события А,В,…,К – единственно возможные, то событие А+В+…+К, состоящее в появлении в рез-те испытания хотя бы одного из этих событий, явл-ся достоверным, его вер-ть = 1 : Р(А+В+…+К)=1 В силу т\ч события А,В,…,К – несовместимые, к ним применима теорема сложения: Р(А+В+…+К)=Р(А)+Р(В)+…+Р(К)=1

Следствие 2: Сумма вер-ей противоположных событий = 1 Р(А)+Р(А )=1 Это следует из т\ч противоположные события образуют полную группу.

Пример 1. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. Решение. Появление цветного шара означает появление либо красного, либо синего шара.

Вероятность появления красного шара (событие А) Р (А) = 10 / 30 = 1 / 3. Вероятность появления синего шара (событие В) Р (В) = 5 / 30 = 1 / 6. События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = l / 3 + l / 6 = l / 2.