
Задание
Период
несущей частоты
![]() =10
мкс.
=10
мкс.
Длительность
импульсов
![]() =50
мкс.
=50
мкс.
Период
следования
![]() =150
мкс.
=150
мкс.
Ослабление
в полосе пропускания
![]() =0,5
дБ.
=0,5
дБ.
Ослабление
в полосе задерживания
![]() =21
дБ.
=21
дБ.
Амплитуда
несущего колебания
![]() =15
В.
=15
В.
Сопротивление
генератора радиоимпульсов и сопротивление
нагрузки
![]() Ом.
Ом.
Характеристика фильтра аппроксимируется полиномом Чебышева.
В ходе выполнения курсовой работы необходимо:
Рассчитать и построить график амплитудного спектра радиоимпульсов.
Определить частоты fп2 и fз2 и рассчитать превышение амплитуды частоты fп2 над амплитудой частоты fз2 в децибелах в виде соотношения А = 20lgUmп/Umз на входе фильтра.
Рассчитать минимально допустимое ослабление фильтра в полосе задерживания Аmin = Апол – А.
Рассчитать порядок m НЧ-прототипа требуемого фильтра.
Получить выражение для передаточной функции НЧ-прототипа при аппроксимации его характеристики полиномом Чебышева.
Осуществить реализацию двухсторонне нагруженного полосового LC-фильтра.
Осуществить реализацию полосового ARC-фильтра.
Привести ожидаемую характеристику ослабления полосового фильтра в зависимости от частоты, т. е. A = K(f).
Рассчитать ослабление ARC-фильтра на границах полосы пропускания и полосы непропускания (задерживания).
Привести схему ARC-полосового фильтра.
Выполнение работы
Расчет амплитудного спектра радиоимпульсов
Несущая
частота
![]() кГц.
кГц.
Частоты нулей огибающей спектра
![]()
![]()
Максимальное
значение огибающей
![]()
Частота
следования
![]()
Частоты
гармоник лежащих справа от
![]()
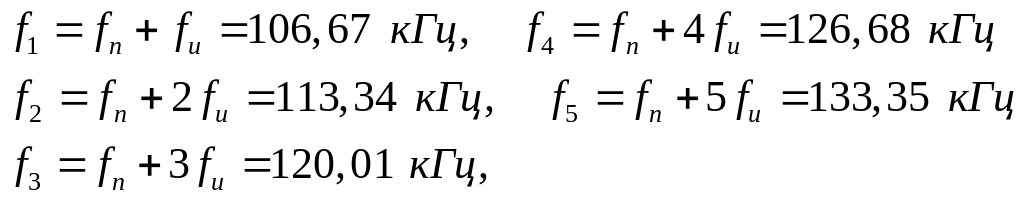
Частоты гармоник лежащих слева от
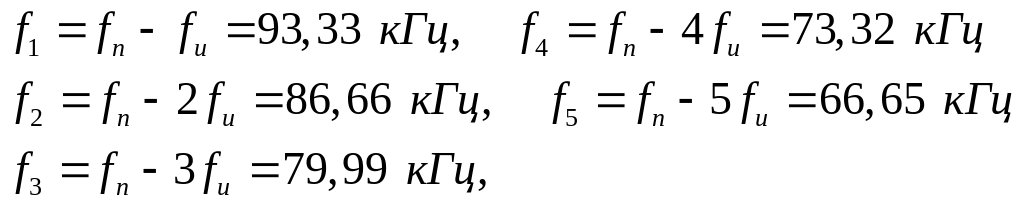
Амплитуды напряжения i-ых гармоник находятся по формуле
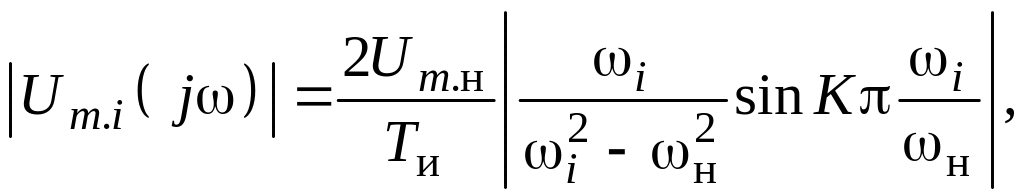
где K = tи/Tн = 5 – количество периодов несущих колебаний косинусоидальной формы в импульсе.
![]() скважность
- целое число, в спектре будут
отсутствовать гармоники с номерами,
кратными скважности.
скважность
- целое число, в спектре будут
отсутствовать гармоники с номерами,
кратными скважности.
Главный «лепесток спектра» занимает диапазон частот от 79,99 до 120,01 кГц.
![]()
F(n)=
U![]()
113,34 кГц 1,097 В
126,68 кГц 0,578 В
86,66 кГц 0,959 В
73,32кГц 0,438 В
После расчета амплитуд, их значения отражаются в виде дискретных составляющих внутри огибающей спектра (рис. 1).

Рис.1
Формирование требований к полосовому фильтру
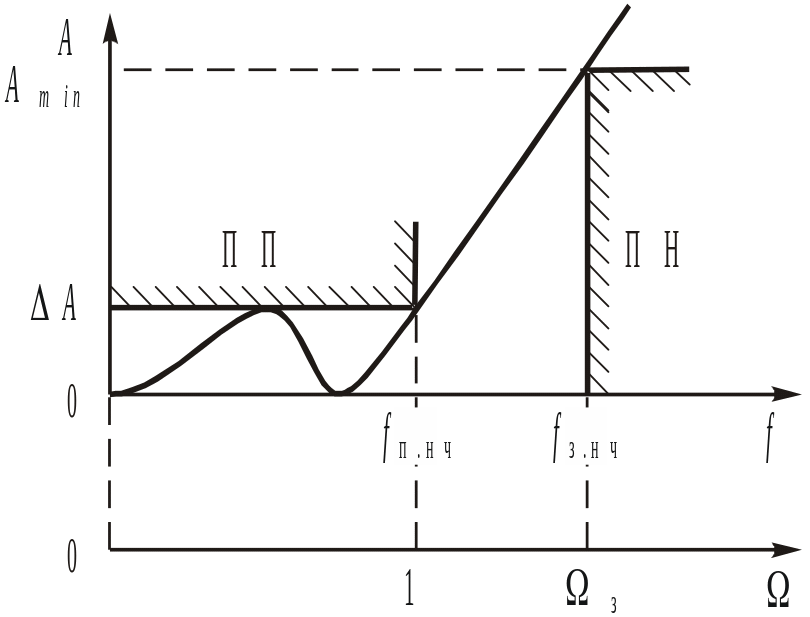
Примем за эффективную часть спектра, которую нужно выделить полосовым фильтром, диапазон частот от 86,66 кГц до 113,34 кГц. Следовательно, эти частоты будут определять частоты границы полосы пропускания фильтра fп1 и fп2 соответственно (рис.2,б). Граничную частоту полосы непропускания fз2 выбираем равной частоте первой гармоники спектра сигнала, находящейся после частоты (fн + 1/tи) = 120 кГц. Этой частотой является частота f4 = 126,68 кГц. Следовательно, fз2 = f4=126,68 кГц.
Найдем центральную частоту ПП:
![]()
![]()
Граничная
частота непропускания
![]() кГц
кГц
На рис. 2 приведены структурные характеристики ослабления фильтра нижних частот (ФНЧ) и полосового фильтра (ПФ).
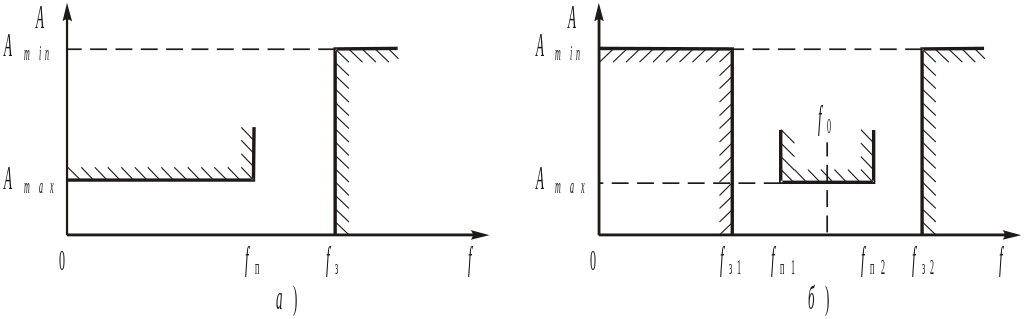

Рис.3 Схема подключения фильтра к источнику сигнала
Минимально-допустимое ослабление фильтра в ПН зависит от разницы амплитуд гармоник f2 и f4 спектра сигнала на выходе фильтра, выраженной в децибелах и заданной величиной Апол – полного ослабления:
где
![]()
А = 20lgUm2/Um4=5,57 дБ
![]() дБ
дБ
Таким образом, требования к полосовому фильтру сводятся к следующему:

Аппроксимация передаточной функции должна быть выполнена с помощью полинома Чебышева.
Формирование передаточной функции нч-прототипа
Определим частоты фильтра прототипа
![]()
![]()
Нормированной частоты фильтра
![]()
![]()
Находим коэффициент неравномерности ослабления фильтра в ПП при A = A и = 1, когда (1) = Тm(1) = 1:
Требования к НЧ-прототипу могут быть проиллюстрированы рисунком 4.
![]()
Порядок фильтра Чебышева при A = Amin и =з, т. е. ослабление рассматривается в полосе непропускания. А в ПН полином Чебышева Тm() = chmarch, поэтому
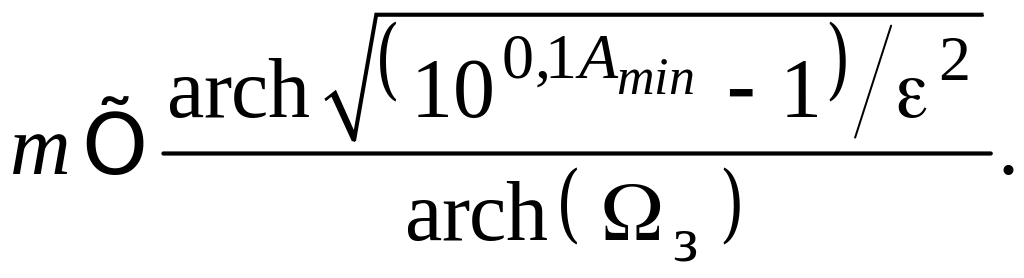
Для вычисления функции archх рекомендуется соотношение
![]()
![]()
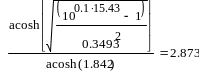
Необходимо взять m=3 порядок низкочастотного фильтра прототипа.
Для
фильтра 3 порядка при
=0,5дБ
полюсами нормированной передаточной
функции
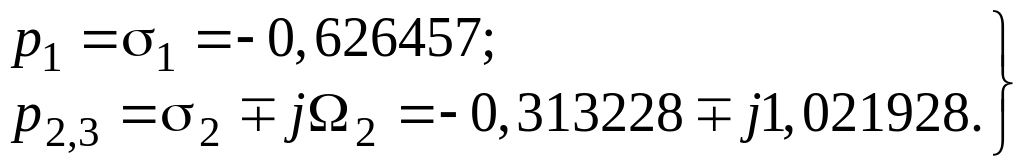
Обращаем внимание на то, что полюсы расположены в левой полуплоскости комплексной переменной р.
Формируем нормированную передаточную функцию НЧ-прототипа в виде
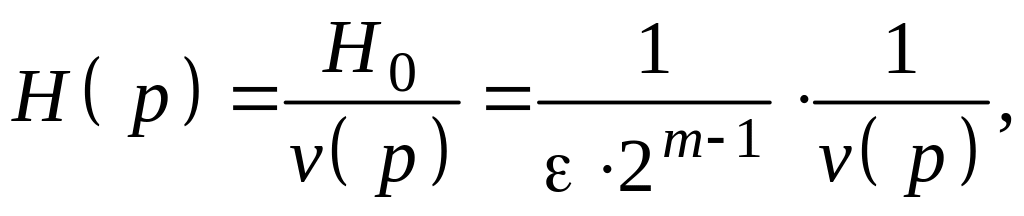
где v(р) – полином Гурвица, который можно записать через полюсы:

Производя вычисления, получим
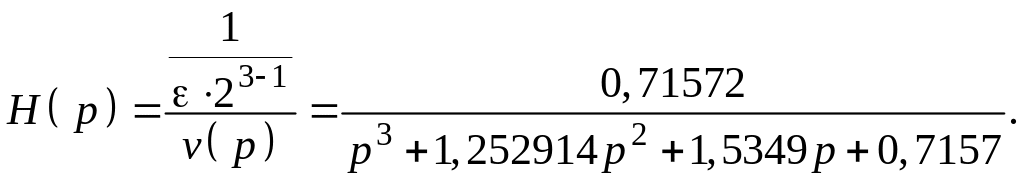
Обращаем внимание на то, что числитель равен свободному члену полинома знаменателя.
Реализация lc-прототипа
Для получения схемы НЧ-прототипа воспользуемся методом Дарлингтона, когда для двусторонне нагруженного фильтра (рис.3) составляется выражение для входного сопротивления Zвх.1(р). Подставляя в него значение v(р) и значение h(p), после преобразований получим
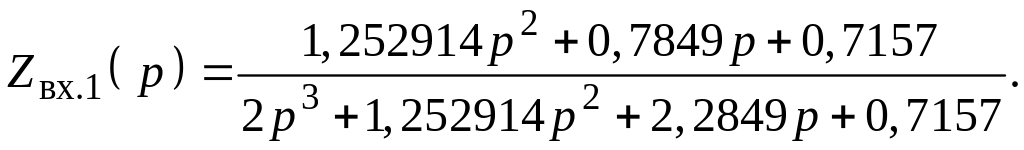
Эта формула описывает входное сопротивление двухполюсника (согласно схеме на рис. 3 фильтр, нагруженный на сопротивление Rн, это действительно двухполюсник). А если известно выражение для входного сопротивления, то можно построить схему двухполюсника, воспользовавшись, например, методом Кауэра. По этому методу формула для Zвх(р) разлагается в непрерывную дробь путем деления полинома числителя на полином знаменателя. При этом степень числителя должна быть больше степени знаменателя. Исходя из последнего, выражение преобразуется к виду
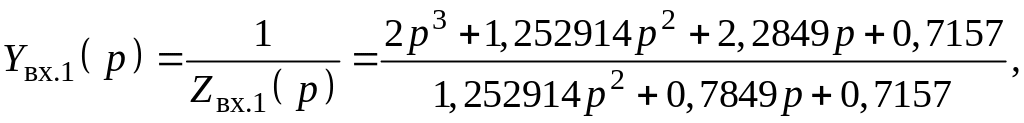
после чего производится ряд последовательных делений. Вначале числитель делим на знаменатель:
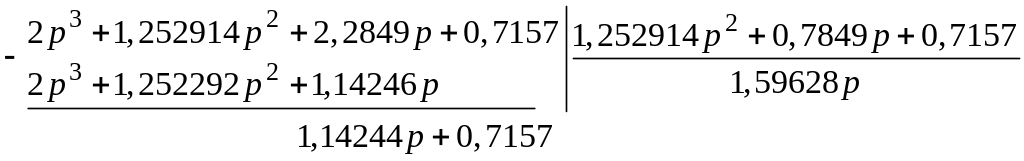
Затем первый делитель делим на первый остаток:
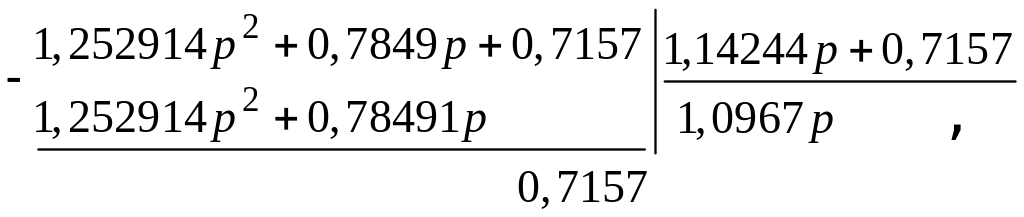
Второй делитель делим на второй остаток:
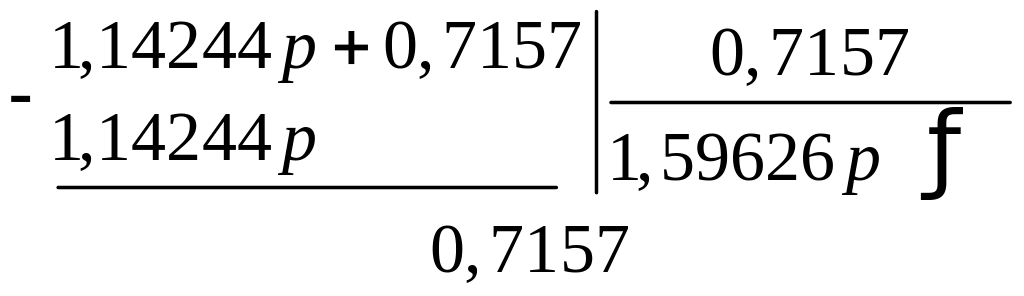
Третий делитель делим на третий остаток:
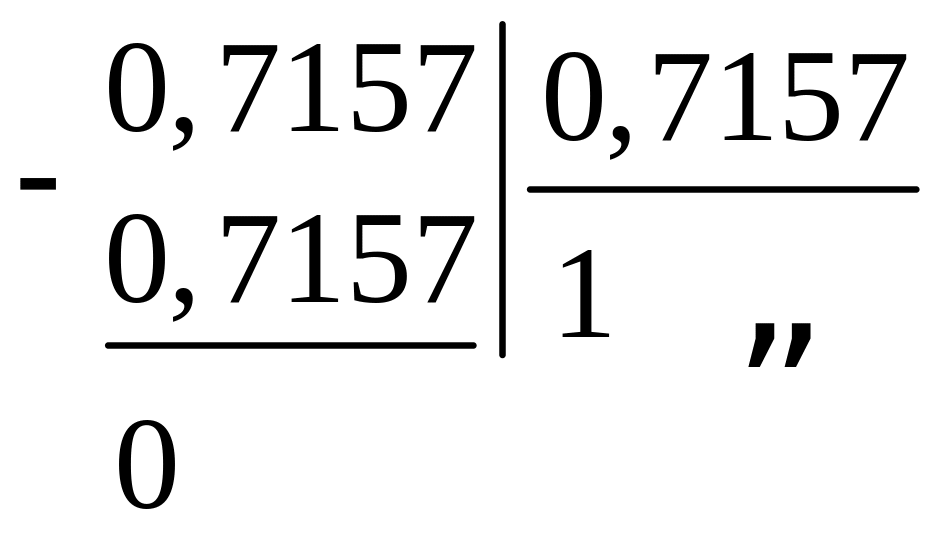
Получили четыре результата деления, которые отражают четыре нормированных по частоте и по сопротивлению элемента схемы в виде значений их проводимостей: pC, 1/pL, 1/R. Из анализа первого результата деления следует, что он отражает емкостную проводимость, поэтому все выражение можно записать в виде цепной дроби:
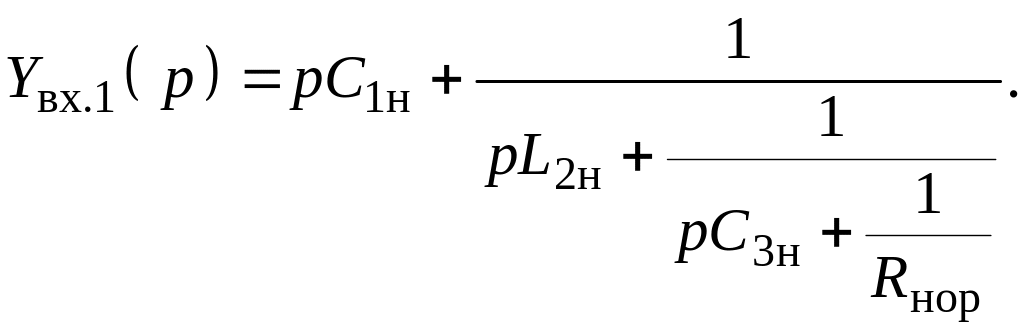
По этой формуле составляем схему (рис. 5), на которой С1н = 1,5963; L2н = 1,097; С3н = 1,5963; Rг.н = Rн.н = Rнор.
Рис.5
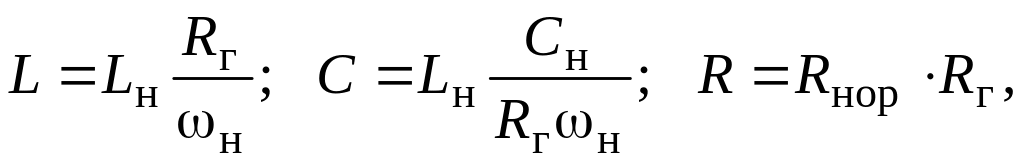
где н = п.нч – нормирующая частота;
Rг –нормирующее сопротивление, равное внутреннему сопротивлению источника сигнала.
Используя данные соотношения и значения н и Rг получаем реальные значения элементов схемы НЧ-прототипа:

![]()
![]() Ф
Ф
![]()
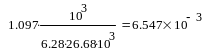 Гн
Гн
![]() Ф
Ф
