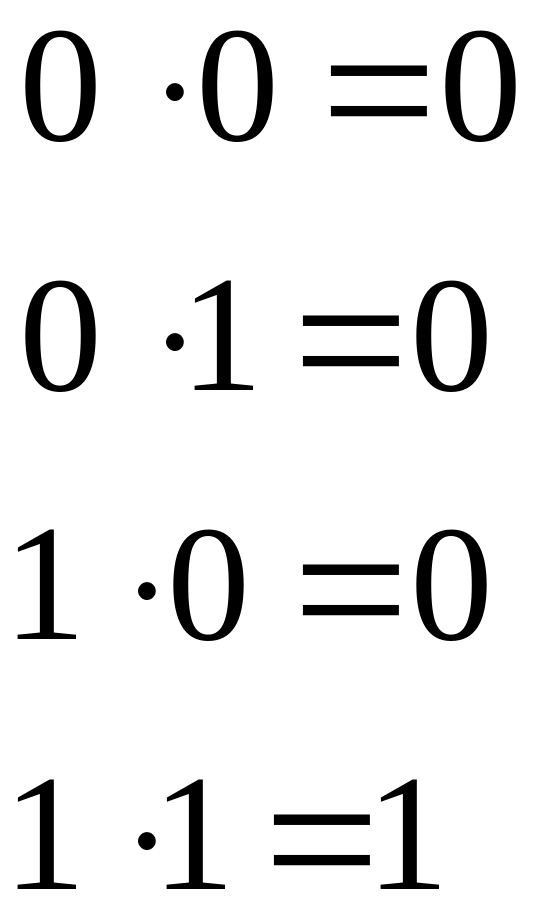Раздел 2. Техническое и программное обеспечение.

Тема 4. Арифметические основы эвм

Системой счисления называют способ наименования и записи чисел.

История: Понятие числа возникло и развивалось вместе с развитием простейших операций над числами – сложением, вычитанием, умножением и делением.

Люди сразу оценили возможность моделирования чисел при помощи камешков, пальцев на руке. Это заметно облегчало арифметические действия. Этот исторический этап счета сохранился: все 1 классники проходят этот путь (считают палочки; счеты и др.).

Стало ясно, что необходимо логически признать бесконечность общего количества чисел из того факта, что нельзя указать самого большого числа (Архимед). В то же время было очевидно, что всеобщая конкретная модель конечна (противоречие между числом и моделью чисел).

Требование: Модель должна обслуживать практические потребности людей, должна содержать достаточно большое число элементов.

Наиболее точной моделью числа является его запись (связана с потребностью запоминать числа).

На протяжении тысячелетий формы записи чисел сильно изменились.

Непозиционная система счислений:

А) римская

I – 1 II – 2 III – 3

IV – 4 V – 5 VI – 6

VII – 7 VIII – 8 IX – 9

X – 10 L – 50 C – 100 D - 500

M – 1000 CCCLXXVIII = 37810

(неудобно производить арифметические вычисления, сложно записывать большие числа).

Аддитивная = сложение

LXVI = 50 + 10 + 5 + 1 = 66₁₀

Но:

N = 5 – 1 = 4 IX = 10 – 1 = 9

XL = 50 – 10 = 40 XC = 100 – 10 = 90

CD = 500 – 100 = 400

Б) славянская (буквы алфавита)

а) десятичная

возникла в Древней Индии, затем проникла в арабскую математику в средние века в Европу.

Последовательность цифр, вклад каждой цифры не только от значения, но и от места (позиции), которое она занимает. Потребовала введения числа 0

Преимущества: 1) Краткость записи чисел по сравнению с непозиционной с.с. (чтобы записать число К, необходимо не более lg K + 1 цифр)

возможность формального сведения арифметических действий над числами к действиям над его цифрами. (правила алгоритма носят общий характер и не зависят от конкретного вида чисел; является «механическим» возможно передать ЭВМ)

Основание с.с. – отношение значений единиц соседних разрядов.

395₁₀ = 300 + 90 + 5 = 3۠۬۬۬۬۬۬ + 9

Запись целого числа N в любой позиционной системе счисления с основанием n обозначает представление этого числа в виде ∑ степеней основания данной системы и с различными коэффициентами, меньшими n (цифры в записи числа)

Пример: 57210

60 = 1 61 = 6 62 = 36 63 = 216 64 = 1296 > 572 отбрас.

целое число N может быть записано в с.с. в натуральным основанием n.

3. Восьмеричная система счисления – позиции системы счисления с основанием 8. Используется набор цифр 0, 1, 2, 3, 4, 5, 6, 7

Запись числа

abcd₈ = , где a, b, c, d < 8

613₈ =

Шестнадцатеричная с.с. – основание = 16

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 = А, 11 = В, 12 = С, 13 = D, 14 = Е, 15 = F

пример:

2258→ 10 17778→ 10 1008→ 10 10010→ 10 2АВС16→ 10 67Е10→ 10 D305C16→ 10

Двоичная с.с. – позиционная система с основанием 2

Цифры: 0, 1 используются ЭВМ

Сравнительная таблица

10	8	16	2
0	0	0000	0000
1	1	1	0001
2	2	2	0010
3	3	3	0011
4	4	4	0100
5	5	5	0101
6	6	6	0110
7	7	7	0111
8	10	8	1000
9	11	9	1001
10	12	А	1010
11	13	B	1011
	14	C	1100
13	15	D	1101
14	16	E	1110
15	17	F	1111
16	20	10	заполнить

Д 305 С₁₆ → ₂ 1101 0011 0000 0101 1100₂ т.к. 16 = 24

11 1110 0110 1111₂ → ₁₆ 3 Е 6 F

Если использовать 8, как промежуточную, то число разделится на триады

(2³ = 8).

1 011 010 101₂ = 1325₈ = 2D5₁₀ =

пример: 101011₂ → ₈→ ₁₆ → ₁₀

111010011₂ → ₈→ ₁₆→ ₁₀

Арифметические операции с двоичной системой счисления

Сложение:

0 + 0 = 0 0 + 1 = 0 1 + 0 = 0 1 + 1 = 10

Вычитание:

0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 10 – 1 = 1

Умножение:

Пример:

1) 101101₂ или 101111₂ = 1011100₂

101101

101111

1011100

2) 1011₂ · 101₂ = 110111₂

1011

101

1011

0000

1 011

110111

3) 1101₂ · 1101₂ = 10101001₂

1101

1101

1101

0000

1101

1101

1 0101001

Самостоятельная работа:

Дать определение информатике

Перечислить устройства ввода информации.

Перевести числа из одной системы счислений в др.