§14. Некоторые свойства дпф.

1) Число отсчетов N сигнала в частотной и временной области одинаково

2) Спектральный коэффициент

3) Если N-четное число и {s(nT)} – вещественные отсчеты, то

где _* - знак комплексного сопряжения,

= 0, 1, 2, 3, … , N/2

При = 0

- вещественный отсчет

Примеры вычисления ДПФ

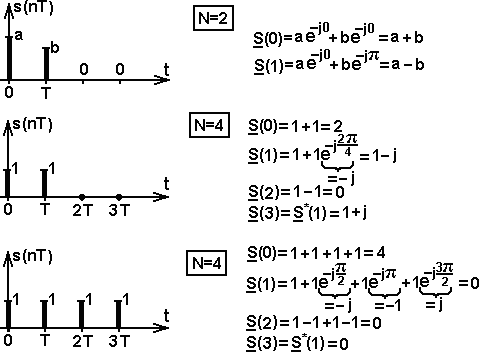
Рис. 21.

§15. Спектральный метод анализа прохождения сигнала через дискретный фильтр.

Этот метод основан на свойстве ДПФ, называемом теоремой свертки: если сигнал s_2T(t) представляет собой свертку дискретного сигнала s_1T(t) и импульсной характеристики g_T(t) дискретного фильтра, то дискретное преобразование Фурье для этой свертки {S₂(k)} находится из соотношения

S₂(k) = S₁(k)^.H(k),

Где

H(k) – дискретное преобразование Фурье от импульсной характеристики ДФ,

{H(k)} – отсчеты комплексного коэффициента передачи ДФ

Порядок вычисления отклика ДФ на сигнал, заданный N своими дискретными отсчетами {S₁(nT)} (n=0, 1, 2, 3, … , N -1), таков:

1) Для заданной последовательности {S₁(nT)} вычисляются N спектральных коэффициентов S₁(k) (k=0, 1, 2, 3, … , N -1)

2) Если задана последовательность отсчетов импульсной характеристики ДФ {g(nТ)}, то для нее находятся спектральные коэффициенты {H(k)}.

Если задан комплексный коэффициент передачи дискретного фильтра Н_Т(ω), то {H(k)} – его дискретные отсчеты.

3) Вычисляются произведения соответствующих спектральных коэффициентов

S₁(k)^.H(k) = S₂(k)

Где {S₂(k)} – спектральные коэффициенты отклика ДФ.

4) По спектральным коэффициентам {S₂(k)} находится обратное ДПФ

5) При необходимости по отсчетам {s₂(nT)} находится дискретный сигнал

Заметим, что при вычислении спектральным методом число отсчетов N берется равным сумме необходимого числа отсчетов воздействия N_s1 и необходимого числа отсчетов импульсной характеристики N_g, то есть

N= N_s1+ N_g

Тогда недостающие отсчеты воздействия и импульсной характеристики считаются нулевыми.

Нетрудно показать, что для нахождения отклика ДФ спектральным методом

Требуется такое же число арифметических операций, что и при временном методе, то есть примерно N². Так что вычислительные трудности при вычислении отклика фильтра в реальном масштабе времени при большом N остаются.

Выход из этой ситуации заключается в переходе от ДПФ к так называемому быстрому преобразованию Фурье (БПФ).

§16. Быстрое преобразование Фурье (бпф)

Сущность быстрого преобразования Фурье заключается в разбиении исходной последовательности отсчетов {s(nT)} объемом N (N считается равным 2^m) на две последовательности (четную и нечетную), для каждой из которых вычисляются ДПФ, а результаты объединяются. Можно показать, что при таком однократном прореживании по времени получается сокращение числа арифметических операций, необходимых для нахождения отклика, примерно в 2 раза.

При необходимости такое прореживание можно проводить многократно, пока в каждой последовательности останутся по 2 отсчета (тогда спектральные коэффициенты находятся путем сложения и вычитания отсчетов).

При таком многократном прореживании получается экономия в числе арифметических операций для нахождения отклика примерно в N / log₂N раз.

Например, при N=2¹⁰=1024, обычное ДПФ требует N² 10⁶ арифметических операций, в то время как при БПФ их требуется примерно в 100 раз меньше.

Заметим, что существенная экономия получается лишь при большом N.

Известен и другой алгоритм реализации БПФ, называемый прореживанием по частоте.

Аналогично алгоритмам реализации прямого БПФ существуют алгоритмы реализации обратного БПФ.